
【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为 . 
【答案】2
【解析】解:∵∠ABC=90°, ∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
在RT△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC= ![]() =5,
=5,
∴PC=OC=OP=5﹣3=2.
∴PC最小值为2.
故选B.
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣ ![]() x+
x+ ![]() 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 .
上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( ) 
A.![]() =
= ![]()
B.![]() =
= ![]()
C.![]() =
= ![]()
D.![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=2,DF=8,则AB的长为______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格见价目表.

若某户居民![]() 月份用水
月份用水![]() ,则应收水费:
,则应收水费:![]() 元.
元.
(1)若该户居民![]() 月份用水
月份用水![]() ,则应收水费______元;
,则应收水费______元;
(2)若该户居民![]() 、
、![]() 月份共用水
月份共用水![]() (
(![]() 月份用水量超过
月份用水量超过![]() 月份),共交水费
月份),共交水费![]() 元,则该户居民
元,则该户居民![]() ,
,![]() 月份各用水多少立方米?
月份各用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,PM、QN分别是AB、AC的垂直平分线,∠BAC=100°那么∠PAQ等于( )

A. 50° B. 40° C. 30° D. 20°
查看答案和解析>>
科目:初中数学 来源: 题型:
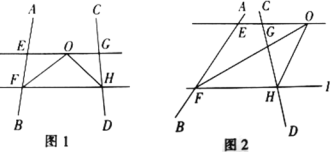
【题目】[探究]如图,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB,CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF= °,∠ FOH= °
(2)若∠AFH+∠CHF= 100°,求∠FOH的度数.
(3)当∠FOH=_____ °时 ,AB//CD.
[拓展]如图,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB,CD交于点E、G.若∠AFH+∠CHF=a,求∠FOH的度数. (用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b﹣a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )![]()
A.甲、乙
B.丙、丁
C.甲、丙
D.乙、丁
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com