Question

21.给定抛物线C：y²=4x,F是C的焦点，过点F的直线l与C相交于A、B两点.

（Ⅰ）设l的斜率为1，求与夹角的大小；

（Ⅱ）设=λ,若λ∈［4,9］，求l在y轴上截距的变化范围.

Answer 1

21.本小题主要考查抛物线的性质，直线与抛物线的关系以及解析几何的基本方法、思想和综合解题能力.

解：（Ⅰ）C的焦点为F（1,0），直线l的斜率为1，

所以l的方程为y=x－1.

将y=x－1代入方程y²=4x,并整理得x²－6x+1=0.

设A（x₁,y₁）,B（x₂,y₂），则有x₁+x₂=6,x₁x₂=1.

·=（x₁,y₁）·（x₂,y₂）=x₁x₂+y₁y₂=2x₁x₂－（x₁+x₂）+1=－3.

||||=·

 ==.

cos〈,〉==－，

所以与夹角的大小为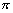－arccos.

（Ⅱ）由题设=λ,得（x₂－1,y₂）=λ（1－x₁,－y₁）,

即

由②得y₂²=λ²y₁².

∵y₁²=4x₁,y₂²=4x₂,

∴x₂=λ²x₁.                                                                         　③

联立①、③解得x₂=λ.依题意有λ>0,

∴B（λ,2）或B（λ,－2）.又F（1,0），

得直线l方程为

（λ－1）y=2（x－1）或（λ－1）y=－2（x－1）.

当λ∈［4,9］时，l在y轴上的截距为或－.

由=,

可知在［4,9］上是递减的，

∴≤≤,－≤－≤－.

直线l在y轴上截距的变化范围为［－,－］∪［,］.