设f(x)=x2-4x=4,x属于【t,t+1](属于r)答案解析
科目:gzsx
来源:
题型:
当实数x,y满足条件|x|+|y|<1时,变量
μ=的取值范围是
(1,3)
(1,3)
.
查看答案和解析>>
科目:gzsx
来源:
题型:
函数f(x)=x2-4x-4.
(1)求f(x)在闭区间[0,3]上的最大值和最小值.
(2)设f(x)在闭区间[t,t+1](t∈R)上的最小值记为g(t),试写出g(t)的函数关系式.
查看答案和解析>>
科目:gzsx
来源:
题型:
设函数y=x
2-4x+3,x∈[-1,4],则f(x)的最小值和最大值为
.
查看答案和解析>>
科目:gzsx
来源:
题型:
.设f(x)=x2-4x-4,x∈[t,t+1](t∈R),求函数f(x)的最小值的解析式,并作出此解析式的图象.
查看答案和解析>>
科目:gzsx
来源:
题型:
设函数y=x
2-4x+3,x∈[-1,4],则f(x)的最大值为
8
8
.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知a
1=1,点(a
n,a
n+1)在函数f(x)=x
2+4x+2的图象上,其中n=1,2,3,4,…
(1)证明:数列{lg(a
n+2)}是等比数列;
(2)设数列{a
n+2}的前n项积为T
n,求T
n及数列{a
n}的通项公式;
(3)已知b
n是
与
的等差中项,数列{b
n}的前n项和为S
n,求证:
≤Sn<.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知等差数列{log
4(a
n-1)}(n∈N
*),且a
1=5,a
3=65,函数f(x)=x
2-4x+4,设数列{b
n}的前n项和为S
n=f(n),
(1)求数列{a
n}与数列{b
n}的通项公式;
(2)记数列c
n=(a
n-1)•b
n,且{c
n}的前n项和为T
n,求T
n;
(3)设各项均不为零的数列{d
n}中,所有满足d
k•d
k+1<0的整数k的个数称为这个数列的异号数,令d
n=
(n∈N
*),试问数列{d
n}是否存在异号数,若存在,请求出;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:
设
f(x)=若存在互异的三个实数x
1,x
2,x
3,使f(x
1)=f(x
2)=f(x
3),则x
1+x
2+x
3的取值范围是
(3,4)
(3,4)
.
查看答案和解析>>
科目:gzsx
来源:
题型:
设f(x)是定义在[-1,1]上的奇函数,g(x)的图象与f(x)的图象关于直线x=1对称,而当x∈[2,3]时,g(x)=-x2+4x-4.
(Ⅰ)求f(x)的解析式;
(Ⅱ)对任意x1,x2∈[0,1],且x1≠x2,求证:|f(x2)-f(x1)|<2|x2-x1|;
(Ⅲ)对任意x1,x2∈[0,1],且x1≠x2,求证:|f(x2)-f(x1)|≤1.
查看答案和解析>>
科目:gzsx
来源:
题型:
设
f(x)=,若存在互异的三个实数x
1,x
2,x
3,使f(x
1)=f(x
2)=f(x
3),则x
1+x
2+x
3的取值范围是( )
查看答案和解析>>
科目:gzsx
来源:2007年北京九中高一数学竞赛试卷(解析版)
题型:解答题
设f(x)是定义在[-1,1]上的奇函数,g(x)的图象与f(x)的图象关于直线x=1对称,而当x∈[2,3]时,g(x)=-x2+4x-4.
(Ⅰ)求f(x)的解析式;
(Ⅱ)对任意x1,x2∈[0,1],且x1≠x2,求证:|f(x2)-f(x1)|<2|x2-x1|;
(Ⅲ)对任意x1,x2∈[0,1],且x1≠x2,求证:|f(x2)-f(x1)|≤1.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年广东省江门市新会一中高三(上)第二次检测数学试卷(文科)(解析版)
题型:解答题
函数f(x)=x2-4x-4.
(1)求f(x)在闭区间[0,3]上的最大值和最小值.
(2)设f(x)在闭区间[t,t+1](t∈R)上的最小值记为g(t),试写出g(t)的函数关系式.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年河南省周口市项城市锦诚高中高二(上)12月月考数学试卷(解析版)
题型:填空题
设函数y=x2-4x+3,x∈[-1,4],则f(x)的最大值为 .
查看答案和解析>>
科目:gzsx
来源:2009-2010学年广东省揭阳市揭西县河婆中学高三(上)11月月考数学试卷(理科)(解析版)
题型:解答题
已知a
1=1,点(a
n,a
n+1)在函数f(x)=x
2+4x+2的图象上,其中n=1,2,3,4,…
(1)证明:数列{lg(a
n+2)}是等比数列;
(2)设数列{a
n+2}的前n项积为T
n,求T
n及数列{a
n}的通项公式;
(3)已知b
n是
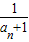
与

的等差中项,数列{b
n}的前n项和为S
n,求证:

.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知等差数列{log4(an-1)}(n∈N*),且a1=5,a3=65,函数f(x)=x2-4x+4,设数列{bn}的前n项和为Sn=f(n),
(1)求数列{an}与数列{bn}的通项公式;
(2)记数列cn=(an-1)•bn,且{cn}的前n项和为Tn,求Tn;
(3)设各项均不为零的数列{dn}中,所有满足dk•dk+1<0的整数k的个数称为这个数列的异号数,令dn=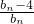 (n∈N*),试问数列{dn}是否存在异号数,若存在,请求出;若不存在,请说明理由.
(n∈N*),试问数列{dn}是否存在异号数,若存在,请求出;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:013
已知f(x)=x2-4x-4,当x∈[t,t+1]时函数f(x)的最小值是t的函数,设为g(t),则当t<1时,g(t)等于
[ ]
A. t2+2t-7 B. t2-2t+7
C. t2-2t-7 D. t2+2t+7
查看答案和解析>>
科目:gzsx
来源:成功之路·突破重点线·数学(学生用书)
题型:044
(1)已知f(x)为二次函数,且f(2x+1)+f(2x-1)=16x2-4x+6,求f(x).
(2)已知函数f(x)=x2+bx+c,对任意实数t都有f(2+t)=f(2-t),试比较f(1),f(2),f(4)的大小.
(3)设f(x)为定义在实数集R上的偶函数,当x≤-1时,y=f(x)的图象经过点(-2,0),斜率为1的射线,又在y=f(x)的图象中有一部分是顶点在(0,2),且经过点(-1,1)的一段抛物线.试求函数f(x)的表达式.
查看答案和解析>>
科目:gzsx
来源:2011年高考数学总复习备考综合模拟试卷(5)(解析版)
题型:解答题
已知等差数列{log
4(a
n-1)}(n∈N
*),且a
1=5,a
3=65,函数f(x)=x
2-4x+4,设数列{b
n}的前n项和为S
n=f(n),
(1)求数列{a
n}与数列{b
n}的通项公式;
(2)记数列c
n=(a
n-1)•b
n,且{c
n}的前n项和为T
n,求T
n;
(3)设各项均不为零的数列{d
n}中,所有满足d
k•d
k+1<0的整数k的个数称为这个数列的异号数,令d
n=
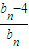
(n∈N
*),试问数列{d
n}是否存在异号数,若存在,请求出;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:不详
题型:解答题
.设f(x)=x2-4x-4,x∈[t,t+1](t∈R),求函数f(x)的最小值的解析式,并作出此解析式的图象.
查看答案和解析>>
科目:gzsx
来源:2009-2010学年广东省华南师大附中高三综合测试数学试卷2(理科)(解析版)
题型:解答题
已知a
1=1,点(a
n,a
n+1)在函数f(x)=x
2+4x+2的图象上,其中n=1,2,3,4,…
(1)证明:数列{lg(a
n+2)}是等比数列;
(2)设数列{a
n+2}的前n项积为T
n,求T
n及数列{a
n}的通项公式;
(3)已知b
n是

与
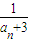
的等差中项,数列{b
n}的前n项和为S
n,求证:
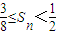
.
查看答案和解析>>

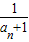 与
与 的等差中项,数列{bn}的前n项和为Sn,求证:
的等差中项,数列{bn}的前n项和为Sn,求证: .
.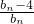 (n∈N*),试问数列{dn}是否存在异号数,若存在,请求出;若不存在,请说明理由.
(n∈N*),试问数列{dn}是否存在异号数,若存在,请求出;若不存在,请说明理由.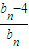 (n∈N*),试问数列{dn}是否存在异号数,若存在,请求出;若不存在,请说明理由.
(n∈N*),试问数列{dn}是否存在异号数,若存在,请求出;若不存在,请说明理由. 与
与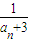 的等差中项,数列{bn}的前n项和为Sn,求证:
的等差中项,数列{bn}的前n项和为Sn,求证: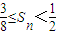 .
.