练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >已知a=（2 1）为矩阵A=（1a-14）

    已知a=（2 1）为矩阵A=（1a-14）答案解析

    科目：gzsx 来源： 题型：

    （2011•闵行区三模）已知椭圆
    x2
    4
    +y2=1    中心为O，右顶点为M，过定点D（t，0）（t≠±2）作直线l交椭圆于A、B两点．
    （1）若直线l与x轴垂直，求三角形OAB面积的最大值；
    （2）若t=
    6
    5
    ，直线l的斜率为1，求证：∠AMB=90°；
    （3）在x轴上，是否存在一点E，使直线AE和BE的斜率的乘积为非零常数？若存在，求出点E的坐标和这个常数；若不存在，说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知n为正整数，规定f1（x）=f（x），fn+1（x）=f（fn（x）），已知f(x)=
    2(1-x)，0≤x≤1
    x-1，
     1＜x≤2
    ，
    （1）解不等式f（x）≤x；
    （2）设集合A={0，1，2}，对任意x∈A，证明：f3（x）=x．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2007•惠州模拟）设n为正整数，规定：fn(x)=
    f{f[…f(x)]}
    n个f
    ，已知f(x)=
    2(1-x)，0≤x≤1
    x-1，1＜x≤2
    ，
    （1）解不等式f（x）≤x；
    （2）设集合A={0，1，2}，对任意x∈A，证明：f3（x）=x；
    （3）求f2007(
    8
    9
    )    的值；
    （4）若集合B={x|f12（x）=x，x∈[0，2]}，证明：B中至少包含8个元素．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设n为正整数，规定：fn(x)=
    f{f[…f(x)…]}
    n个f
    ，已知f(x)=
    2(1-x)
    x-1
    ，
    ，
    (0≤x≤1)
    (1＜x≤2)
    ．
    （1）解不等式：f（x）≤x；
    （2）设集合A={0，1，2}，对任意x∈A，证明：f3（x）=x；
    （3）探求f2009(
    8
    9
    )    ；
    （4）若集合B={x|f12（x）=x，x∈[0，2]}，证明：B中至少包含有8个元素．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知双曲线
    x2
    24tanα
    -
    y2
    16cotα
    =1（α为锐角）和圆（x-m）2+y2=r2相切于点A（4
    		3
    ，4），求α，m，r的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知椭圆
    x2
    4
    +y2=1    中心为O，右顶点为M，过定点D（t，0）（t≠±2）作直线l交椭圆于A、B两点．
    （1）若直线l与x轴垂直，求三角形OAB面积的最大值；
    （2）若t=
    6
    5
    ，直线l的斜率为1，求证：∠AMB=90°；
    （3）直线AM和BM的斜率的乘积是否为非零常数？请说明理由．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知复数z=
    2+i
    x-i
    为纯虚数，其中i虚数单位，则实数x的值为（　　）

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    （2009•卢湾区一模）将奇函数的图象关于原点（即（0，0））对称这一性质进行拓广，有下面的结论：
    ①函数y=f（x）满足f（a+x）+f（a-x）=2b的充要条件是y=f（x）的图象关于点（a，b）成中心对称．
    ②函数y=f（x）满足F（x）=f（x+a）-f（a）为奇函数的充要条件是y=f（x）的图象关于点（a，f（a））成中心对称（注：若a不属于x的定义域时，则f（a）不存在）．
    利用上述结论完成下列各题：
    （1）写出函数f（x）=tanx的图象的对称中心的坐标，并加以证明．
    （2）已知m（m≠-1）为实数，试问函数f(x)=
    x+m
    x-1
    的图象是否关于某一点成中心对称？若是，求出对称中心的坐标并说明理由；若不是，请说明理由．
    （3）若函数f(x)=(x-
    2
    3
    )(|x+t|+|x-3|)-4    的图象关于点(
    2
    3
    ，f(
    2
    3
    ))    成中心对称，求t的值．

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    设n为正整数，规定：fn(x)=
    f{f[…f(x)…]}
    n个f
    ，已知f(x)=
    2(1-x)(0≤x≤1)
    x-1(1＜x≤2)
    ．
    （1）解不等式：f（x）≤x；
    （2）设集合A={0，1，2}，对任意x∈A，证明：f3（x）=x；
    （3）求f2008(
    8
    9
    )    的值．

    查看答案和解析>>

    科目：gzsx 来源：2013届湖北省高二上学期期中考试理科数学 题型：选择题

    已知x2+y 2 = 1 ,若x + y －k ≥0对符合条件一切x 、y都成立,则实数k的最大值为（  ）

        A．          B．0            C．－             D．1

     

    查看答案和解析>>

    科目：gzsx 来源：2010-2011学年宁夏高三第三次月考理科数学试卷 题型：选择题

    已知向量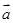=(－2,1)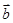，=(－3，0)，则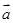在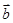方向上的投影为(   )

    A．－2            B． C．2          D．－

     

    查看答案和解析>>

    科目：gzsx 来源： 题型：解答题

    将奇函数的图象关于原点（即（0，0））对称这一性质进行拓广，有下面的结论：
    ①函数y=f（x）满足f（a+x）+f（a-x）=2b的充要条件是y=f（x）的图象关于点（a，b）成中心对称．
    ②函数y=f（x）满足F（x）=f（x+a）-f（a）为奇函数的充要条件是y=f（x）的图象关于点（a，f（a））成中心对称（注：若a不属于x的定义域时，则f（a）不存在）．
    利用上述结论完成下列各题：
    （1）写出函数f（x）=tanx的图象的对称中心的坐标，并加以证明．
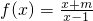    （2）已知m（m≠-1）为实数，试问函数数学公式的图象是否关于某一点成中心对称？若是，求出对称中心的坐标并说明理由；若不是，请说明理由．
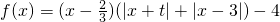    （3）若函数数学公式的图象关于点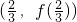数学公式成中心对称，求t的值．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：解答题

    设n为正整数，规定：fn(x)=
    f{f[…f(x)…]}
    n个f
    ，已知f(x)=
    2(1-x)(0≤x≤1)
    x-1(1＜x≤2)
    ．
    （1）解不等式：f（x）≤x；
    （2）设集合A={0，1，2}，对任意x∈A，证明：f3（x）=x；
    （3）求f2008(
    8
    9
    )    的值．

    查看答案和解析>>

    科目：gzsx 来源：福建 题型：解答题

    已知双曲线
    x2
    24tanα
    -
    y2
    16cotα
    =1（α为锐角）和圆（x-m）2+y2=r2相切于点A（4
    		3
    ，4），求α，m，r的值．

    查看答案和解析>>

    科目：gzsx 来源：惠州模拟 题型：解答题

    设n为正整数，规定：fn(x)=
    f{f[…f(x)]}
    n个f
    ，已知f(x)=
    2(1-x)，0≤x≤1
    x-1，1＜x≤2
    ，
    （1）解不等式f（x）≤x；
    （2）设集合A={0，1，2}，对任意x∈A，证明：f3（x）=x；
    （3）求f2007(
    8
    9
    )    的值；
    （4）若集合B={x|f12（x）=x，x∈[0，2]}，证明：B中至少包含8个元素．

    查看答案和解析>>

    科目：gzsx 来源：卢湾区一模 题型：解答题

    将奇函数的图象关于原点（即（0，0））对称这一性质进行拓广，有下面的结论：
    ①函数y=f（x）满足f（a+x）+f（a-x）=2b的充要条件是y=f（x）的图象关于点（a，b）成中心对称．
    ②函数y=f（x）满足F（x）=f（x+a）-f（a）为奇函数的充要条件是y=f（x）的图象关于点（a，f（a））成中心对称（注：若a不属于x的定义域时，则f（a）不存在）．
    利用上述结论完成下列各题：
    （1）写出函数f（x）=tanx的图象的对称中心的坐标，并加以证明．
    （2）已知m（m≠-1）为实数，试问函数f(x)=
    x+m
    x-1
    的图象是否关于某一点成中心对称？若是，求出对称中心的坐标并说明理由；若不是，请说明理由．
    （3）若函数f(x)=(x-
    2
    3
    )(|x+t|+|x-3|)-4    的图象关于点(
    2
    3
    ，f(
    2
    3
    ))    成中心对称，求t的值．

    查看答案和解析>>

    科目：gzsx 来源：2010年上海市卢湾区高考数学一模试卷（文理合卷）（解析版） 题型：解答题

    将奇函数的图象关于原点（即（0，0））对称这一性质进行拓广，有下面的结论：
    ①函数y=f（x）满足f（a+x）+f（a-x）=2b的充要条件是y=f（x）的图象关于点（a，b）成中心对称．
    ②函数y=f（x）满足F（x）=f（x+a）-f（a）为奇函数的充要条件是y=f（x）的图象关于点（a，f（a））成中心对称（注：若a不属于x的定义域时，则f（a）不存在）．
    利用上述结论完成下列各题：
    （1）写出函数f（x）=tanx的图象的对称中心的坐标，并加以证明．
    （2）已知m（m≠-1）为实数，试问函数的图象是否关于某一点成中心对称？若是，求出对称中心的坐标并说明理由；若不是，请说明理由．
    （3）若函数的图象关于点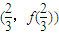成中心对称，求t的值．

    查看答案和解析>>

    科目：gzsx 来源：宝山区模拟 题型：解答题

    设n为正整数，规定：fn(x)=
    f{f[…f(x)…]}
    n个f
    ，已知f(x)=
    2(1-x)
    x-1
    ，
    ，
    (0≤x≤1)
    (1＜x≤2)
    ．
    （1）解不等式：f（x）≤x；
    （2）设集合A={0，1，2}，对任意x∈A，证明：f3（x）=x；
    （3）探求f2009(
    8
    9
    )    ；
    （4）若集合B={x|f12（x）=x，x∈[0，2]}，证明：B中至少包含有8个元素．

    查看答案和解析>>

    科目：gzsx 来源：不详 题型：单选题

    已知复数z=
    2+i
    x-i
    为纯虚数，其中i虚数单位，则实数x的值为（　　）
    A．-
    1
    2
    		B．
    1
    2
    		C．2D．1

    查看答案和解析>>

    科目：gzsx 来源： 题型：

    已知点M(2,3),P为抛物线上的一动点,F为焦点,则PF+PM取最小值时,点P的坐标是

    A. (0,1)           B. (1,1)        C. (2,1)           D.(3,)

    查看答案和解析>>