如图抛物线y=x2+bx+c交y轴与B.对称轴是x=2求抛物解析答案解析
科目:czsx
来源:2006年湖南省常德市初中毕业生学业考试数学试卷
题型:059
如下图,在直角坐标系中,以点A(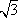 ,0)为圆心,以
,0)为圆心,以 为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.
为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.
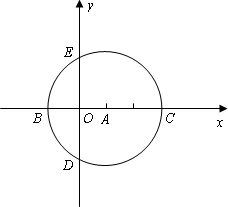
(1)若抛物线y= x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上.
x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上.
(2)在(1)中的抛物线的对称轴上求一点P,使得△PBD的周长最小.
(3)设Q为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点M,使得四边形BCQM是平行四边形.若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 已知抛物线y=-x2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
已知抛物线y=-x2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
(1)求抛物线的函数解析式;
(2)画出函数的图象与对称轴,设Q是抛物线的对称轴上的任意一点,以Q为圆心,QB长为半径作圆,过坐标原点O作⊙Q的切线OC,C为切点,求OC的长;
(3)特别地,要使切点C′恰好在抛物线上,应如何确定点C′的位置和圆心Q′的位置?简述你的作法并在图中把⊙Q′与切线OC′作出来(要求用尺规作图,保留作图痕迹,写作法,但不用证明).
查看答案和解析>>
科目:czsx
来源:1997年广西中考数学试卷(解析版)
题型:解答题
已知抛物线y=-x
2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
(1)求抛物线的函数解析式;
(2)画出函数的图象与对称轴,设Q是抛物线的对称轴上的任意一点,以Q为圆心,QB长为半径作圆,过坐标原点O作⊙Q的切线OC,C为切点,求OC的长;
(3)特别地,要使切点C′恰好在抛物线上,应如何确定点C′的位置和圆心Q′的位置?简述你的作法并在图中把⊙Q′与切线OC′作出来(要求用尺规作图,保留作图痕迹,写作法,但不用证明).

查看答案和解析>>
科目:czsx
来源:
题型:
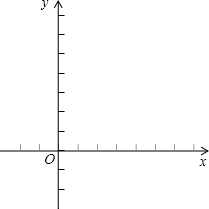
(1997•广西)已知抛物线y=-x
2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
(1)求抛物线的函数解析式;
(2)画出函数的图象与对称轴,设Q是抛物线的对称轴上的任意一点,以Q为圆心,QB长为半径作圆,过坐标原点O作⊙Q的切线OC,C为切点,求OC的长;
(3)特别地,要使切点C′恰好在抛物线上,应如何确定点C′的位置和圆心Q′的位置?简述你的作法并在图中把⊙Q′与切线OC′作出来(要求用尺规作图,保留作图痕迹,写作法,但不用证明).
查看答案和解析>>
科目:czsx
来源:2012届浙江省兰溪市柏社中学九年级下学期独立作业数学卷(带解析)
题型:解答题
已知抛物线y=﹣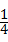 x2+bx+c的对称轴为直线x=1,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.△ABC的面积等于1.5.
x2+bx+c的对称轴为直线x=1,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.△ABC的面积等于1.5.
(1)请求出抛物线的解析式,并求出点A的坐标.
(2)在抛物线上是否存在点M,使得△MAB的面积等于△ABC的面积.如果存在,求出符合条件的点M的坐标;如果不存在,请说明理由.
(3)点P在抛物线上,直线PQ∥BC交x轴于点Q,连接BQ.
①若含45°角的直角三角板如图2所示放置.其中,一个顶点与点C重合,直角顶点D在BQ上,另一 个顶点E在PQ上.请求出此时点Q的坐标和直线BQ的函数解析式;
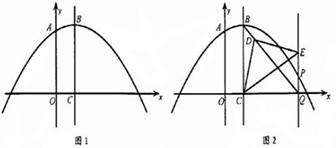
②若含30°角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标.
查看答案和解析>>
科目:czsx
来源:2011-2012学年浙江省兰溪市九年级下学期独立作业数学卷(解析版)
题型:解答题
已知抛物线y=﹣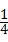 x2+bx+c的对称轴为直线x=1,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.△ABC的面积等于1.5.
x2+bx+c的对称轴为直线x=1,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.△ABC的面积等于1.5.
(1)请求出抛物线的解析式,并求出点A的坐标.
(2)在抛物线上是否存在点M,使得△MAB的面积等于△ABC的面积.如果存在,求出符合条件的点M的坐标;如果不存在,请说明理由.
(3)点P在抛物线上,直线PQ∥BC交x轴于点Q,连接BQ.
①若含45°角的直角三角板如图2所示放置.其中,一个顶点与点C重合,直角顶点D在BQ上,另一
个顶点E在PQ上.请求出此时点Q的坐标和直线BQ的函数解析式;
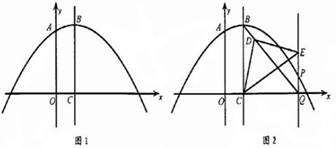
②若含30°角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标.
查看答案和解析>>
科目:czsx
来源:2011年辽宁省营口市初中毕业升学考试数学试卷
题型:044
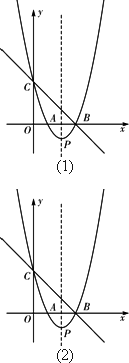
如图,直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
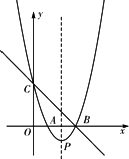
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点M,使以C、P、M为顶点的三角形为等腰三角形?若存在,请直接写出所有符合条件的点M的坐标;若不存在,请说明理由;
(3)连结AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由;
(4)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值.(图(1)、图(2)供画图探究)
查看答案和解析>>
科目:czsx
来源:
题型:
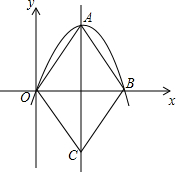
如果一条抛物线y=ax
2+bx+c(a≠0)与x轴有两个交点,那么以这两个交点和该抛物线的顶点、对称轴上一点为顶点的菱形称为这条抛物线的“抛物菱形”.
(1)若抛物线y=ax
2+bx+c(a≠0)与x轴的两个交点为(-1,0)、
(3,0),且这条抛物线的“抛物菱形”是正方形,求这条抛物线的函数解析式;
(2)如图,四边形OABC是抛物线y=-x
2+bx(b>0)的“抛物菱形”,且∠OAB=60°
①求“抛物菱形OABC”的面积.
②将直角三角板中含有“60°角”的顶点与坐标原点O重合,两边所在直线与“抛物菱形OABC”的边AB、BC交于E、F,△OEF的面积是否存在最小值,若存在,求出此时△OEF的面积;若不存在,说明理由.
查看答案和解析>>
科目:czsx
来源:2017届天津市河东区九年级上期末数学试卷(解析版)
题型:解答题
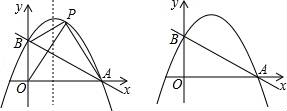
如图,直线y=﹣ x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一点,连接PA、PB、PO,若△POA的面积是△POB面积的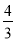 倍.
倍.
①求点P的坐标;
②点Q为抛物线对称轴上一点,请直接写出QP+QA的最小值;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
查看答案和解析>>
科目:czsx
来源:2006年初中数学总复习下册
题型:044
已知:如图,直径为10的⊙M交x轴于A、B两点,圆心M的坐标为(3,0),⊙M与y轴的负半轴交于点C,抛物线y=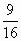 x2+bx+c经过点C,且与x轴交于D、E两点,A点在此抛物线的对称轴上.
x2+bx+c经过点C,且与x轴交于D、E两点,A点在此抛物线的对称轴上.

(1)求此抛物线的解析式;
(2)在x轴的正半轴上是否存在点P,使以点P、O、C为顶点的三角形与△AOC相似?如果存在,求出点P的坐标;如果不存在,说明理由;
(3)判断过D、G两点的直线与⊙M的位置关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
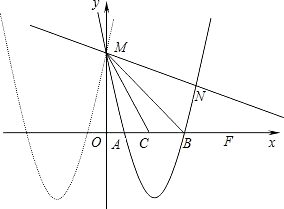
如图,已知抛物线y=mx
2+nx+p与y=x
2+6x+5关于y轴对称,与y轴交于点M,与x轴交于点A和B.
(1)求出y=mx
2+nx+p的解析式,试猜想出与一般形式抛物线y=ax
2+bx+c关于y轴对称的二次函数解析式(不要求证明);
(2)若A,B的中点是点C,求sin∠CMB;
(3)如果过点M的一条直线与y=mx
2+nx+p图象相交于另一点N(a,b),a≠b且满足a
2-a+q=0,b
2-b+q=0(q为常数),求点N的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知直线y=
x+1与y轴交于点A,与x轴交于点D,抛物线y=
x
2+bx+c与直线交于A、
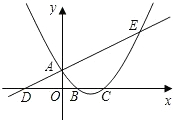
E两点,与x轴交于B、C两点,且B点坐标为(1,0).
(1)求该抛物线的解析式;
(2)动点P在x轴上移动,当△PAE是直角三角形时,求点P的坐标P;
(3)在抛物线的对称轴上找一点M,使|AM-MC|的值最大,求出点M的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,抛物线
y=-x2+x+3与x轴相交于点A、B,与y轴相交于点C,顶点为点D,对称轴l与直线BC相交于点E

,与x轴相交于点F.
(1)求直线BC的解析式;
(2)设点P为该抛物线上的一个动点,以点P为圆心,r为半径作⊙P
①当点P运动到点D时,若⊙P与直线BC相交,求r的取值范围;
②若r=
,是否存在点P使⊙P与直线BC相切?若存在,请求出点P的坐标;若不存在,请说明理由.
提示:抛物线y=ax
2+bx+x(a≠0)的顶点坐标(
-,),对称轴x=
-.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,抛物线
y=-x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于
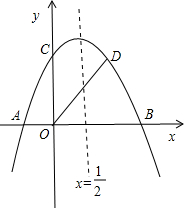
点C,对称轴为直线
x=,OA=2,OD平分∠BOC交抛物线于点D(点D在第一象限).
(1)求抛物线的解析式和点D的坐标;
(2)在抛物线的对称轴上,是否存在一点P,使得△BPD的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)点M是抛物线上的动点,在x轴上是否存在点N,使A、D、M、N四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的M点坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
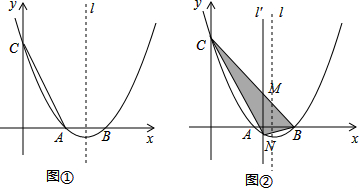
如图①所示,抛物线y=x
2+bx+c与x轴交于A,B两点,与y轴交于点C(0,2),连接AC,若tan∠OAC=2.
(1)求抛物线对应的二次函数的解析式;
(2)在抛物线的对称轴l上是否存在点P,使∠APC=90°?若存在,求出点P的坐标;若不存在,请说明理由
(3)如图②所示,连接BC,M是线段BC上(不与B、C重合)的一个动点,过点M作直线l′∥l,交抛物线于点N,连接CN、BN,设点M的横坐标为t.当t为何值时,△BCN的面积最大?最大面积为多少?
查看答案和解析>>
科目:czsx
来源:
题型:
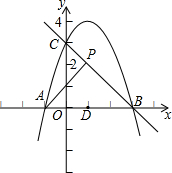
如图,直线y=-x+3与x轴,y轴分别交于B,C两点,抛物线y=-x
2+bx+c经过点B和点C,点A是抛物线与x轴的另一个交点.
(1)求抛物线的解析式和顶点坐标;
(2)若点Q在抛物线的对称轴上,能使△QAC的周长最小,请求出Q点的坐标;
(3)若直线l:y=kx(k≠0)与线段BC交于点D(不与点B,C重合),则是否存在这样的直线l,使得以B,O,D为顶点的三角形与△BAC相似?若存在,求出该直线的函数表达式及点D的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
如图,直线y=-x+3与x轴,y轴分别交于B,C两点,抛物线y=-x
2+bx+c经过点B和点C,点A
是抛物线与x轴的另一个交点.
(1)求抛物线的解析式和顶点坐标;
(2)若点Q在抛物线的对称轴上,能使△QAC的周长最小,请求出Q点的坐标;
(3)在直线BC上是否存在一点P,且s
△PAC:S
△PAB=1:3?若存在,求P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,抛物线
y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式;
(2)作Rt△OBC的高OD,延长OD与抛物线在第一象限内交于点E,求点E的坐标;
(3)①在x轴上方的抛物线上,是否存在一点P,使四边形OBEP是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由;
②在抛物线的对称轴上,是否存在上点Q,使得△BEQ的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,抛物线
y=x2-mx+n与y轴交于点C(0,-4),与x轴交于点A(-2,0)
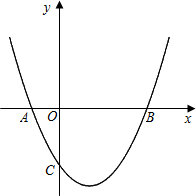
和点B(点B在点A的右侧).
(1)求抛物线的解析式及点B的坐标;
(2)若点P、Q分别从B、C两点同时出发,均以每秒1个长度单位的速度沿BA、CO方向运动,当P运动到A时P、Q两点同时停止运动.在运动过程中,设运动的时间为t(秒),△APQ的面积为S,求S与t之间的函数关系式,并写出自变量t的取值范围.
[提示:抛物线y=ax
2+bx+c(a≠0)的对称轴
是
x=-,顶点坐标是
(-,)].
查看答案和解析>>
科目:czsx
来源:
题型:
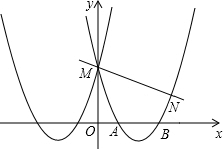
如图,已知抛物线y=mx
2+nx+p与y=x
2+6x+5关于y轴对称,并与y轴交于点M,与x轴交于点A和B.
(1)求出y=mx
2+nx+p的解析式,试猜想出一般形式y=ax
2+bx+c(a≠0)关于y轴对称的二次函数解析式(不要求证明);
(2)若AB的中点是C,求sin∠CMB;
(3)如果一次函数y=kx+b(k≠0)过点M,且与抛物线y=mx
2+nx+p,相交于另一点N(i,j),如果i≠j,且i
2-j
2-i+j=0,求k的值.
查看答案和解析>>

![]() ,0)为圆心,以
,0)为圆心,以![]() 为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.
为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.
![]() x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上.
x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上. 已知抛物线y=-x2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
已知抛物线y=-x2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
 (1997•广西)已知抛物线y=-x2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).
(1997•广西)已知抛物线y=-x2+bx-12与x轴相交于A(m,0)、B(n,0)两点,其中m、n满足(m-1)(n-1)-5=0(m≠n).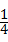 x2+bx+c的对称轴为直线x=1,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.△ABC的面积等于1.5.
x2+bx+c的对称轴为直线x=1,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.△ABC的面积等于1.5.
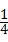 x2+bx+c的对称轴为直线x=1,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.△ABC的面积等于1.5.
x2+bx+c的对称轴为直线x=1,此抛物线与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.△ABC的面积等于1.5.


 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以这两个交点和该抛物线的顶点、对称轴上一点为顶点的菱形称为这条抛物线的“抛物菱形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以这两个交点和该抛物线的顶点、对称轴上一点为顶点的菱形称为这条抛物线的“抛物菱形”. x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.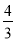 倍.
倍.
![]() x2+bx+c经过点C,且与x轴交于D、E两点,A点在此抛物线的对称轴上.
x2+bx+c经过点C,且与x轴交于D、E两点,A点在此抛物线的对称轴上.
 如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,与y轴交于点M,与x轴交于点A和B.
如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,与y轴交于点M,与x轴交于点A和B. E两点,与x轴交于B、C两点,且B点坐标为(1,0).
E两点,与x轴交于B、C两点,且B点坐标为(1,0). ,与x轴相交于点F.
,与x轴相交于点F. 点C,对称轴为直线x=
点C,对称轴为直线x=

 是抛物线与x轴的另一个交点.
是抛物线与x轴的另一个交点. 如图,抛物线y=-
如图,抛物线y=- 和点B(点B在点A的右侧).
和点B(点B在点A的右侧). 如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,并与y轴交于点M,与x轴交于点A和B.
如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,并与y轴交于点M,与x轴交于点A和B.