
题目列表(包括答案和解析)
 ),若线段RS绕原点O逆时针旋转90°,求线段RS所经过区域的面积(重复经过的区域面积不重复计算).
),若线段RS绕原点O逆时针旋转90°,求线段RS所经过区域的面积(重复经过的区域面积不重复计算).
| x2+1 |
| (4-x)2+4 |
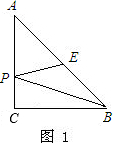
 某课题组在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决下列问题:
某课题组在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决下列问题:| x2+1 |
| (4-x)2+4 |
 某课题组在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决下列问题:
某课题组在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决下列问题: (0≤x≤4)的最小值.
(0≤x≤4)的最小值. (2011•金东区模拟)在平面直角坐标系xOy中,
(2011•金东区模拟)在平面直角坐标系xOy中,| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com