
ΓΨΧβΡΩΓΩΡ≥Βγ ”Χ®ΈΣΝΥΫβ±ΨΒΊ«χΒγ ”ΫΎΡΩΒΡ ’ ”«ιΩωΘ§Ε‘≤ΩΖ÷Ιψ÷ίΩΣ’ΙΝΥΓΑΡψΉνœ≤Α°ΒΡΒγ ”ΫΎΡΩΓ±ΒΡΈ ΨμΒς≤ιΘ®ΟΩ»Υ÷ΜΧν–¥“ΜœνΘ©Θ§ΗυΨί ’Φ·ΒΡ ΐΨίΜφ÷ΤΝΥœ¬ΟφΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§ΗυΨί“Σ«σΜΊ¥πœ¬Ν–Έ ΧβΘΚ
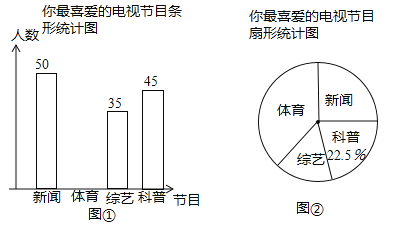
Θ®1Θ©±Ψ¥ΈΈ ΨμΒς≤ιΙ≤Βς≤ιΝΥ ΟϊΙέ÷ΎΘΜ
Θ®2Θ©ΆΦΔΎ÷–Ήνœ≤Α°ΓΑ–¬Έ≈ΫΎΡΩΓ±ΒΡ»Υ ΐ’ΦΒς≤ιΉή»Υ ΐΒΡΑΌΖ÷±»ΈΣ Θ§ΓΑΉέ“’ΫΎΡΩΓ±‘Ύ…»–ΈΆ≥ΦΤΆΦ÷–ΥυΕ‘”ΠΒΡ‘≤–ΡΫ«ΒΡΕ» ΐΈΣ ΘΜ
Θ®3Θ©≤Ι»ΪΆΦΔΌ÷–ΒΡΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®4Θ©œ÷”–Ήνœ≤Α°ΓΑ–¬Έ≈ΫΎΡΩΓ±Θ®Φ«ΈΣ![]() Θ©Θ§ΓΑΧε”ΐΫΎΡΩΓ±Θ®Φ«ΈΣ
Θ©Θ§ΓΑΧε”ΐΫΎΡΩΓ±Θ®Φ«ΈΣ![]() Θ©Θ§ΓΑΉέ“’ΫΎΡΩΓ±Θ®Φ«ΈΣCΘ©Θ§ΓΑΩΤΤ’ΫΎΡΩΓ±Θ®Φ«ΈΣDΘ©ΒΡΙέ÷ΎΗς“ΜΟϊΘ§Βγ ”Χ®“Σ¥”ΥΡ»Υ÷–ΥφΜζ≥ι»ΓΝΫ»Υ≤ΈΦ”ΝΣ“ξΜνΕ·Θ§«κ”ΟΝ–±μΜρΜ≠ ςΉ¥ΆΦΒΡΖΫΖ®Θ§«σ≥ω«ΓΚΟ≥ιΒΫΉνœ≤Α°ΓΑBΓ±ΚΆΓΑCΓ±ΝΫΈΜΙέ÷ΎΒΡΗ≈¬ Θ°
Θ©Θ§ΓΑΉέ“’ΫΎΡΩΓ±Θ®Φ«ΈΣCΘ©Θ§ΓΑΩΤΤ’ΫΎΡΩΓ±Θ®Φ«ΈΣDΘ©ΒΡΙέ÷ΎΗς“ΜΟϊΘ§Βγ ”Χ®“Σ¥”ΥΡ»Υ÷–ΥφΜζ≥ι»ΓΝΫ»Υ≤ΈΦ”ΝΣ“ξΜνΕ·Θ§«κ”ΟΝ–±μΜρΜ≠ ςΉ¥ΆΦΒΡΖΫΖ®Θ§«σ≥ω«ΓΚΟ≥ιΒΫΉνœ≤Α°ΓΑBΓ±ΚΆΓΑCΓ±ΝΫΈΜΙέ÷ΎΒΡΗ≈¬ Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©200ΘΜΘ®2Θ©40%Θ§63ΓψΘΜΘ®3Θ©ΉςΆΦΦϊΫβΈωΘΜΘ®4Θ©![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ©”Οœ≤ΜΕΩΤΤ’ΫΎΡΩΒΡ»Υ ΐ≥ΐ“‘ΥϋΥυ’ΦΒΡΑΌΖ÷±»Φ¥Ω…ΒΟΒΫΒς≤ιΒΡΉή»Υ ΐΘΜ
Θ®2Θ©”Οœ≤Α°ΓΑ–¬Έ≈ΫΎΡΩΓ±ΒΡ»Υ ΐ≥ΐ“‘Βς≤ιΉή»Υ ΐΒΟΒΫΥϋΥυ’ΦΒΡΑΌΖ÷±»Θ§»ΜΚσ”Ο360Ε»≥Υ“‘œ≤ΜΕΓΑΉέ“’ΫΎΡΩΓ±ΒΡ»Υ ΐΥυ’ΦΒΡΑΌΖ÷±»ΒΟΒΫΉέ“’ΫΎΡΩΓ±‘Ύ…»–ΈΆ≥ΦΤΆΦ÷–ΥυΕ‘”ΠΒΡ‘≤–ΡΫ«ΒΡΕ» ΐΘΜ
Θ®3Θ©”ΟΒς≤ιΒΡΉή»Υ ΐΖ÷±πΦθ»Ξœ≤ΜΕ–¬Έ≈ΓΔΉέ“’ΓΔΩΤΤ’ΒΡ»Υ ΐΒΟΒΫœ≤ΜΕΧε”ΐΒΡ»Υ ΐΘ§»ΜΚσ≤Ι»ΪΆΦΔΌ÷–ΒΡΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®4Θ©Μ≠ ςΉ¥ΆΦ’Ι ΨΥυ”–12÷÷Β»Ω…ΡήΒΡΫαΙϊ ΐΘ§‘Ό’“≥ω≥ιΒΫΉνœ≤Α°ΓΑBΓ±ΚΆΓΑCΓ±ΝΫΈΜΙέ÷ΎΒΡΫαΙϊ ΐΘ§»ΜΚσΗυΨίΗ≈¬ ΙΪ Ϋ«σΫβΘ°
‘ΧβΫβΈωΘΚΘ®1Θ©±Ψ¥ΈΈ ΨμΒς≤ιΙ≤Βς≤ιΒΡΙέ÷Ύ ΐΈΣ45Γ¬22.5%=200Θ®»ΥΘ©ΘΜ
Θ®2Θ©ΆΦΔΎ÷–Ήνœ≤Α°ΓΑ–¬Έ≈ΫΎΡΩΓ±ΒΡ»Υ ΐ’ΦΒς≤ιΉή»Υ ΐΒΡΑΌΖ÷±»ΈΣ50Γ¬200=40%ΘΜΓΑΉέ“’ΫΎΡΩΓ±‘Ύ…»–ΈΆ≥ΦΤΆΦ÷–ΥυΕ‘”ΠΒΡ‘≤–ΡΫ«ΒΡΕ» ΐΈΣ360ΓψΓΝ![]() =63ΓψΘΜ
=63ΓψΘΜ
Ι ¥πΑΗΈΣΘΚ200Θ§40%Θ§63ΓψΘΜ
Θ®3Θ©Ήνœ≤Α°ΓΑ–¬Έ≈ΫΎΡΩΓ±ΒΡ»Υ ΐΈΣ200©¹50©¹35©¹45=70Θ®»ΥΘ©Θ§»γΆΦΘΚ

Θ®4Θ©Μ≠ ςΉ¥ΆΦΈΣΘΚ

Ι≤”–12÷÷Β»Ω…ΡήΒΡΫαΙϊ ΐΘ§«ΓΚΟ≥ιΒΫΉνœ≤Α°ΓΑBΓ±ΚΆΓΑCΓ±ΝΫΈΜΙέ÷ΎΒΡΫαΙϊ ΐΈΣ2Θ§Υυ“‘«ΓΚΟ≥ιΒΫΉνœ≤Α°ΓΑBΓ±ΚΆΓΑCΓ±ΝΫΈΜΙέ÷ΎΒΡΗ≈¬ =![]() =
=![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏyΘΫax2ΘΪbxΘΪc(aΓΌ0)”κx÷αΫΜ”ΎΒψA(Θ≠2Θ§0)Θ§B(1Θ§0)Θ§÷±œΏxΘΫΘ≠0.5”κ¥Υ≈ΉΈοœΏΫΜ”ΎΒψCΘ§”κx÷αΫΜ”ΎΒψMΘ§‘Ύ÷±œΏ…œ»ΓΒψDΘ§ ΙMDΘΫMCΘ§Ν§Ϋ”ACΘ§BCΘ§ADΘ§BDΘ§Ρ≥Ά§―ßΗυΨίΆΦœσ–¥≥ωœ¬Ν–Ϋα¬έΘΚ

ΔΌaΘ≠bΘΫ0ΘΜΔΎΒ±Θ≠2<x<1 ±Θ§y>0ΘΜΔέΥΡ±Ώ–ΈACBD «Νβ–ΈΘΜΔή9aΘ≠3bΘΪc>0Θ§
Ρψ»œΈΣΤδ÷–’ΐ»ΖΒΡ «( )
A. ΔΎΔέΔή B. ΔΌΔΎΔή C. ΔΌΔέΔή D. ΔΌΔΎΔέ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“Μ‘ΣΕΰ¥ΈΖΫ≥Χx2©¹ax+6=0Θ§≈δΖΫΚσΈΣΘ®x©¹3Θ©2=3Θ§‘ρa= Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏ![]() ΒΡΕΞΒψ‘Ύx÷α…œΘ§”κy÷αΫΜ”ΎΒψAΘ§ΫΪ≈ΉΈοœΏ―Ίy÷αΖΫœρœρœ¬ΤΫ“ΤΘ§ ΙΤΫ“ΤΚσΒΡ≈ΉΈοœΏ”κy÷αΫΜ”ΎΒψBΘ§«“
ΒΡΕΞΒψ‘Ύx÷α…œΘ§”κy÷αΫΜ”ΎΒψAΘ§ΫΪ≈ΉΈοœΏ―Ίy÷αΖΫœρœρœ¬ΤΫ“ΤΘ§ ΙΤΫ“ΤΚσΒΡ≈ΉΈοœΏ”κy÷αΫΜ”ΎΒψBΘ§«“![]() .
.
Θ®1Θ©«σcΒΡ÷ΒΘΜ
Θ®2Θ©«σΤΫ“ΤΚσΒΡ≈ΉΈοœΏΒΡΕΞΒψΉχ±ξ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»ΐΫ«–ΈΒΡ»ΐΧθ________________ΫΜ”Ύ“ΜΒψΘ§’βΗωΒψΫ–Ήω»ΐΫ«–ΈΒΡ÷Ί–Ρ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡΨΫ≥ ΠΗΒΨβΡΨΝœ ±Θ§“ΜΑψœ»‘ΎΡΨΑε…œΜ≠≥ωΝΫΗωΒψΘ§»ΜΚσΙΐ’βΝΫΒψΒΟ≥ω“ΜΧθΡΪœΏΘ§’β «ΗυΨί ΐ―ß‘≠άμ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΨίΥ’÷ί»’±®±®ΒάΘ§2010Ρξ1‘¬11»’Υ’÷ί –ΒΡΉνΗΏΤχΈ¬ «5ΓφΘ°ΉνΒΆΤχΈ¬ «©¹2ΓφΘ§Β±ΧλΥ’÷ί –ΒΡΤχΈ¬tΘ®ΓφΘ©ΒΡ±δΜ·ΖΕΈß”Ο≤ΜΒ» Ϋ±μ ΨΈΣ________
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒψPΘ®©¹3Θ§4Θ©ΒΫx÷αΒΡΨύάκ «Θ®ΓΓΓΓΘ©
A. ©¹3B. 3C. 4D. 5
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com