
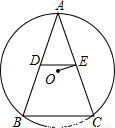
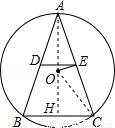
如图,已知⊙0是△ABC的外接圆,半径长为5,点D、E分别是边AB和边AC是中点,AB=AC,BC=6.求∠OED的正切值.
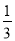 .
.
【解析】
试题分析:连接AO并延长交BC于点H,连接OC,先根据AB=AC得出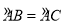 ,根据垂径定理得出OH及AH的长,由锐角三角函数的定义得出tan∠HAC=tan∠OAE=
,根据垂径定理得出OH及AH的长,由锐角三角函数的定义得出tan∠HAC=tan∠OAE=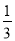 ,再根据D、E分别是边AB和边AC的中点,得出DE∥BC,根据直角三角形的性质得出∠OAE+∠AED=90°,∠AED+∠OED=90°,故可得出∠OAE=∠OED,进而得出结论.
,再根据D、E分别是边AB和边AC的中点,得出DE∥BC,根据直角三角形的性质得出∠OAE+∠AED=90°,∠AED+∠OED=90°,故可得出∠OAE=∠OED,进而得出结论.
试题解析:连接AO并延长交BC于点H,连接OC,
∵AB=AC,
∴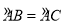 ,
,
∵O为圆心,
∴AH⊥BC,BH=HC,
∴HC=3,
∵半径OC=5,
∴OH=4,AH=9,
∴在Rt△AHC中,tan∠HAC=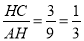 ,即tan∠OAE=
,即tan∠OAE=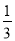 ,
,
∵D、E分别是边AB和边AC的中点,
∴DE∥BC,
∴AH⊥DE,
∴∠OAE+∠AED=90°,
∵E是边AC的中点,O为圆心,
∴OE⊥AC,
∴∠AED+∠OED=90°,
∴∠OAE=∠OED,
∴tan∠OED=tan∠OAE=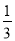 .
.
考点:1.垂径定理;2.三角形中位线定理;3.圆周角定理;4.解直角三角形.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源:2013-2014学年上海市浦东新区中考二模数学试卷(解析版) 题型:填空题
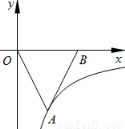
如图,已知点A在反比例函数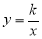 的图像上,点B在x轴的正半轴上,且△OAB是面积为
的图像上,点B在x轴的正半轴上,且△OAB是面积为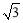 的等边三角形,那么这个反比例函数的解析式是 .
的等边三角形,那么这个反比例函数的解析式是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市松江区中考二模数学试卷(解析版) 题型:选择题
下面计算正确的是( )
A.x3+x2=x5 B.x3•x2=x6 C.x3-x2=x D.x3÷x2=x
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市杨浦区5月中考二模数学试卷(解析版) 题型:填空题
如果将点(-b,-a)称为点(a,b)的“反称点”,那么点(a,b)也是点(-b,-a)的“反称点”,此时,称点(a,b)和点(-b,-a)是互为“反称点”.容易发现,互为“反称点”的两点有时是重合的,例如(0,0)的“反称点”还是(0,0).请再写出一个这样的点:
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市普陀区中考二模数学试卷(解析版) 题型:填空题
Rt△ABC中,∠C=90°,AC=5,BC=12,如果以点C为圆心,r为半径,且⊙C与斜边AB仅有一个公共点,那么半径r的取值范围是
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市徐汇区中考二模数学试卷(解析版) 题型:选择题
一次函数y=2x+1的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com