Question

半径为1，2，3的三个圆两两外切，并且这三个圆都内切于⊙O，则⊙O的半径等于________．

Answer 1

6
分析：由题意半径为1，2，3的三个圆两两外切作图，如图CA=4，CB=3，AB=5得△OAB为直角三角形．再画出坐标，连接OA、OC、OB，所以OA=r-3、OC=r-1、OB=r-2．作OM⊥AC，ON⊥BC，再由勾股定理得OA²=OM²+AM²同理OB²=ON²+BN²，OC²=ON²+CN²．可得r=6，即⊙O的半径为6．
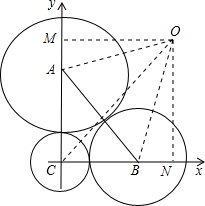
解答：解：如图所示，由题意⊙C，⊙A，⊙B的半径分别为1、3、2，
∴CA=4，CB=3，AB=5．
∵CA²+CB²=AB²，
∴△OAB为直角三角形，CA⊥CB，
画出坐标如图，O是所求圆的圆心设半径为r，连接OA、OC、OB，
∴OA=r-3、OC=r-1、OB=r-2，
A（0，4），B（3，0），C（0，0），
设O（x，y），过O作OM⊥AC，ON⊥BC，
则OA²=OM²+AM²即（r-3）²=x²+（y-4）²，①
同理OB²=ON²+BN²即（r-2）²=y²+（x-3）²，②
OC²=ON²+CN²即（r-1）²=y²+x²，③
由①②③式得r=6，x=3，y=4，
∴⊙O的半径等于6．
点评：这道题考查了相切圆的性质和勾股定理，以及坐标求解法的应用，同学们应熟练掌握，这能更有效地提高做题效率．