
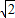 ,∠CAB=45°,点O在BA上移动,以O为圆心作⊙O,使⊙O与边BC相切,切点为D,设⊙O的半径为x,四边形AODC的面积为y.
,∠CAB=45°,点O在BA上移动,以O为圆心作⊙O,使⊙O与边BC相切,切点为D,设⊙O的半径为x,四边形AODC的面积为y.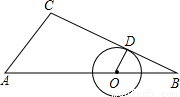
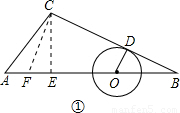 解:(1)如图①,过点C作CE⊥AB,垂足为E.
解:(1)如图①,过点C作CE⊥AB,垂足为E.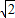 ,∠CAB=45°,
,∠CAB=45°,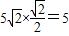 .
.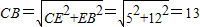 .(2分)
.(2分)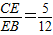 .
.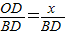 =tanB=
=tanB=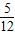 ,
,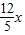 .(4分)
.(4分)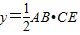 -
- =
=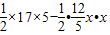 =
=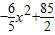 ;(6分)
;(6分)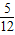 =
=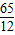 .
.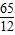 .(9分)
.(9分)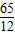 不扣分;
不扣分;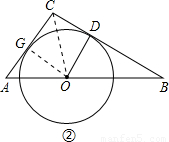
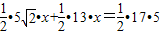 .
.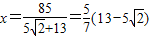 .(12分)
.(12分)

科目:初中数学 来源:2004年全国中考数学试题汇编《二次函数》(04)(解析版) 题型:解答题
 ,顶点为
,顶点为 .
.
查看答案和解析>>
科目:初中数学 来源:2004年山东省枣庄市中考数学试卷(解析版) 题型:解答题
 ,顶点为
,顶点为 .
.
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《四边形》(01)(解析版) 题型:选择题

查看答案和解析>>
科目:初中数学 来源:2004年山东省枣庄市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年山东省枣庄市中考数学试卷(解析版) 题型:选择题

 cm
cm πcm
πcm查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com