
ij��˾Ӫ��A��B���ֲ�Ʒ�������г����У�����������Ϣ��
��Ϣ1������A�ֲ�Ʒ�������������Ԫ�������۲�Ʒx���֣�֮����ڶ��κ�����ϵ ��
��
��x��1ʱ������1.4����x��3ʱ������3.6��
��Ϣ2������B�ֲ�Ʒ�������������Ԫ�������۲�Ʒx���֣�֮�����������������ϵ ��
��
����������Ϣ������������⣺
��1������κ�������ʽ��
��2���ù�˾������A��B���ֲ�Ʒ��10�֣������һ��Ӫ��������ʹ����A��B���ֲ�Ʒ��õ�����֮�������������Ƕ��٣�
��1��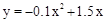
��2������A��Ʒ6�֣�����B��Ʒ4�֣�����A��B���ֲ�Ʒ��õ�����֮��������������6.6��Ԫ��
������������1������1��1.4������3��3.6������ ���ⷽ�������a��b��ֵ���ɵö��κ�������ʽ��
���ⷽ�������a��b��ֵ���ɵö��κ�������ʽ��
��2����������A��B���ֲ�Ʒ��õ�����֮���빺��A��Ʒ����֮��ĺ�����ϵʽ��Ӧ�ö��κ�������ֵԭ����⡣
�⣺��1������1��1.4������3��3.6������ ����
����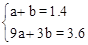 �����
�����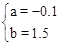 ��
��
����κ�������ʽΪ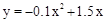 ��
��
��2���蹺��A��Ʒm�֣�����B��Ʒ10��m�֣�����A��B���ֲ�Ʒ��õ�����֮��ΪW��Ԫ����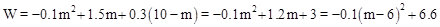
��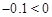 ���൱m��6ʱ��W�����ֵ6.6��
���൱m��6ʱ��W�����ֵ6.6��
���A��Ʒ6�֣�����B��Ʒ4�֣�����A��B���ֲ�Ʒ��õ�����֮��������������6.6��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪������y1=ax2+bx+c��a��0���Ķ��������ǣ�1��4��������ֱ��y2=x+1��һ������ĺ�����Ϊ2��
��1���������ߵĽ���ʽ��
��2���ڸ���������ϵ�л���������y1=ax2+bx+c��a��0����ֱ��y2=x+1��ͼ������ͼ��ֱ��д��ʹ��y1��y2��x��ȡֵ��Χ��
��3������������x����ұ߽���ΪA������A��x��Ĵ��ߣ���ֱ��y2=x+1�ڵ�B����P���������ϣ���S��PAB��6ʱ�����P�ĺ�����x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�٣���?ABCD�У�AB=13��BC=50��BC���ϵĸ�Ϊ12����P�ӵ�B��������B��A��D��A�˶�����B��A�˶�ʱ���ٶ�Ϊÿ��13����λ���ȣ���A��D��A�˶�ʱ���ٶ�Ϊÿ��8����λ���ȣ���Q�ӵ� B������BC�����˶����ٶ�Ϊÿ��5����λ���ȣ�P��Q����ͬʱ����������Q�����Cʱ��P��Q����ͬʱֹͣ�˶������P���˶�ʱ��Ϊt���룩������PQ��
��1������P��A��D��A�˶�ʱ����AP�ij����ú�t�Ĵ���ʽ��ʾ����
��2������AQ���ڵ�P��B��A��D�˶������У�����P���B����A���غ�ʱ���ǡ�APQ�����ΪS����S��t֮��ĺ�����ϵʽ��
��3������Q��QR��AB����AD�ڵ�R������BR����ͼ�ڣ��ڵ�P��B��A��D�˶������У����߶�PQɨ����ͼ�Σ���Ӱ���֣����߶�BR�ֳ������ȵ�������ʱt��ֵ��
��4�����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬ֱ��д��C��D���BCʱt��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У������� ������A��
������A�� ��0���͵�B��1��
��0���͵�B��1�� ������x�����һ������ΪC��
������x�����һ������ΪC��
��1���������ߵĺ�������ʽ��
��2����D�ڶԳ�����Ҳ࣬x���Ϸ����������ϣ��ҡ�BDA=��DAC�����D�����ꣻ
��3���ڣ�2���������£�����BD���������߶Գ����ڵ�E������AE��
���ж��ı���OAEB����״����˵�����ɣ�
�ڵ�F��OB���е㣬��M��ֱ��BD��һ�����㣬�ҵ�M���B���غϣ�����BMF= ��MFOʱ����ֱ��д���߶�BM�ij���
��MFOʱ����ֱ��д���߶�BM�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����֪����ABCΪ�߳���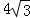 �ĵȱ������Σ��ı���DEFGΪ�߳���6�������Σ��ֽ��ȱߡ�ABC��������DEFG����ͼ1�ķ�ʽ�ڷţ�ʹ��C���E�غϣ���B��C��E����F��ͬһ��ֱ���ϣ���ABC��ͼ1��λ�ó�������ÿ��1����λ���ȵ��ٶ���EF�������������˶�������C���F�غ�ʱ��ͣ�˶������ABC���˶�ʱ��Ϊt�루t��0����
�ĵȱ������Σ��ı���DEFGΪ�߳���6�������Σ��ֽ��ȱߡ�ABC��������DEFG����ͼ1�ķ�ʽ�ڷţ�ʹ��C���E�غϣ���B��C��E����F��ͬһ��ֱ���ϣ���ABC��ͼ1��λ�ó�������ÿ��1����λ���ȵ��ٶ���EF�������������˶�������C���F�غ�ʱ��ͣ�˶������ABC���˶�ʱ��Ϊt�루t��0����
��1���������˶������У���ȱߡ�ABC��������DEFG�ص����ֵ����ΪS����ֱ��д��S��t֮��ĺ�����ϵʽ��
��2����ͼ2������A���D�غ�ʱ������ABE�Ľ�ƽ����BM��AE��M�㣬����ABM�Ƶ�A��ʱ����ת��ʹ��AB���AC�غϣ��õ���ACN�����߶�AG���Ƿ����H�㣬ʹ�á�ANHΪ���������Σ�������ڣ�������߶�EH�ij��ȣ��������ڣ���˵�����ɣ�
��3����ͼ3�����ı���DEFGΪ�߳�Ϊ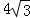 �������Σ���ABC���ƶ��ٶ�Ϊÿ��
�������Σ���ABC���ƶ��ٶ�Ϊÿ�� ����λ���ȣ������������ֲ��䣮��ABC��ʼ�ƶ���ͬʱ��Q���F�㿪ʼ��������FG��GD��ÿ��
����λ���ȣ������������ֲ��䣮��ABC��ʼ�ƶ���ͬʱ��Q���F�㿪ʼ��������FG��GD��ÿ�� ����λ���ȿ�ʼ�ƶ�����ABCֹͣ�˶�ʱ��Q��Ҳֹͣ�˶��������˶������У�DE������BA��AC��P�㣬���Ƿ����t��ֵ��ʹ��PC��EQ�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
����λ���ȿ�ʼ�ƶ�����ABCֹͣ�˶�ʱ��Q��Ҳֹͣ�˶��������˶������У�DE������BA��AC��P�㣬���Ƿ����t��ֵ��ʹ��PC��EQ�������ڣ������t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����������x�ύ��A��B���㣬��y�ύC�㣬��A������Ϊ��2��0������C������Ϊ��0��3�����ĶԳ�����ֱ��

��1���������ߵĽ���ʽ��
��2��M���߶�AB�ϵ�����һ�㣬����MBCΪ����������ʱ����M������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪������ �Ķ���A��2��0������y��Ľ���ΪB��0����1����
�Ķ���A��2��0������y��Ľ���ΪB��0����1����
��1���������ߵĽ���ʽ��
��2���ڶԳ����Ҳ�����������ҳ�һ��C��ʹ��BCΪֱ����Բ���������ߵĶ���A���������C�������Լ���ʱԲ��Բ��P������꣮
��3���ڣ�2���Ļ����ϣ���ֱ��x=t��0<t<10���������߽��ڵ�N����tΪ��ֵʱ����BCN��������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ���ѡ��
����������y�� ������������y��mx��ͼ����ͼ��ʾ���ɴ˿��Եõ�����
������������y��mx��ͼ����ͼ��ʾ���ɴ˿��Եõ����� ��mx��ʵ����Ϊ�� ��
��mx��ʵ����Ϊ�� ��
| A��x��-2 | B��x��1 | C��x1��2��x2����2 | D��x1��1��x2����2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ���ѡ��
��֪��A��1��y1����B��2��y2����C��-3��y3�����ڷ���������y�� ��ͼ���ϣ���y1��y2��y3�Ĵ�С��ϵ�ǣ�������
��ͼ���ϣ���y1��y2��y3�Ĵ�С��ϵ�ǣ�������
| A��y3��y1��y2 |
| B��y1��y2��y3 |
| C��y2��y1��y3 |
| D��y3��y2��y1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com