
【题目】如图,在□ABCD中,已知AB>BC.
(1)实践与操作:作∠ADC的平分线交AB于点E,在DC上截取DF=AD,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形AEFD的形状,并给予证明.

【答案】(1)详见解析;(2)四边形ABEF是菱形,理由详见解析.
【解析】试题分析:(1)由角平分线的作法容易得出结果,在AD上截取AF=AB,连接EF;画出图形即可;(2)由平行四边形的性质和角平分线得出∠BAE=∠AEB,证出BE=AB,由(1)得:AF=AB,得出BE=AF,即可得出结论.
试题解析:解:(1)如图所示:

(2)四边形ABEF是菱形;理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB,
由(1)得:AF=AB,
∴BE=AF,
又∵BE∥AF,
∴四边形ABEF是平行四边形,
∵AF=AB,
∴四边形ABEF是菱形.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
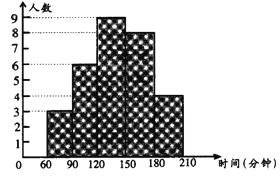
【题目】某校教导处为了了解本校初二学生一天中做家庭作业所用的大致时间(时间以整数记,单位:分钟),对本校的初二学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图所示),请结合统计图中提供的信息,回答下列问题:
(1)本次所抽取样本的容量是多少?
(2)在被调查的学生中,一天做家庭作业所用的大致时间超过120分钟(不包括120分钟)的人数占被调查学生总人数的百分之几?
(3)这次调查得到的所有数据的中位数落在了五个时间段中的哪一段内?
查看答案和解析>>
科目:初中数学 来源: 题型:
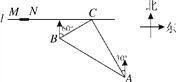
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠一盒乒乓球;乙店的优惠办法是:全部商品按定价的9折出售.某班需购买乒乓球拍4副,乒乓球若干盒(不少于4盒).

(1)当购买乒乓球的盒数为x盒时,在甲店购买需付款 元?在乙店 购买需付款 元?(用含x的代数式表示)
(2)当购买乒乓球盒数为10盒时,去哪家商店购买较合算?请计算说明.
(3) 当购买乒乓球盒数为10盒时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.

(1)图中除直角和平角外,还有相等的角吗?请写出两对:
① ;② .
(2)如果∠AOD=40°,求∠COP和∠BOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
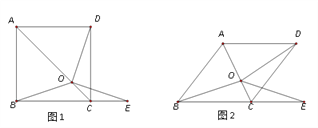
【题目】如图1,在正方形ABCD中,O是对角线AC上一点,点E在BC的延长线上,且OE = OB.
(1)求证:△OBC ≌ △ODC.
(2)求证:∠DOE = ∠ABC.
(3)把正方形ABCD改为菱形,其他条件不变(如图2),若∠ABC = 52° ,求∠DOE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com