
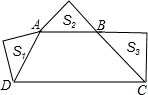
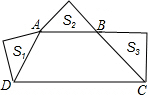
 梯形ABCD中AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向形外作等腰直角三角形,其面积分别是S1、S2、S3,且S1+S3=9S2,则CD=
梯形ABCD中AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向形外作等腰直角三角形,其面积分别是S1、S2、S3,且S1+S3=9S2,则CD=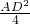 ,S2,=
,S2,=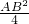 ,S3=
,S3=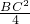 ,结合已知条件推出AD2+BC2=9AB2,因为AD2+BC2=(DC-AB)2,所以代入化简得:CD=4AB,CD=-2AB(不符合题意,舍去),即可答案选D.
,结合已知条件推出AD2+BC2=9AB2,因为AD2+BC2=(DC-AB)2,所以代入化简得:CD=4AB,CD=-2AB(不符合题意,舍去),即可答案选D.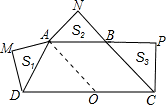 解:如图,作AO∥BC交DC于O点,AB∥CD,∠ADC+∠BCD=90°,
解:如图,作AO∥BC交DC于O点,AB∥CD,∠ADC+∠BCD=90°, AM×MD=
AM×MD= AM2,
AM2,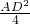 ,
, ,2AN2=AB2,∴S2=
,2AN2=AB2,∴S2=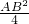 ,
, ,2BP2=BC2,∴S3=
,2BP2=BC2,∴S3=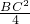 ,
, ,
,

 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
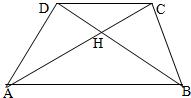 27、梯形ABCD中AB∥CD,对角线AC、BD垂直相交于H,M是AD上的点,MH所在直线交BC于N.在以上前提下,试将下列设定中的两个作为题设,另一个作为结论组成一个正确的命题,并证明这个命题.①AD=BC;②MN⊥BC;③AM=DM.
27、梯形ABCD中AB∥CD,对角线AC、BD垂直相交于H,M是AD上的点,MH所在直线交BC于N.在以上前提下,试将下列设定中的两个作为题设,另一个作为结论组成一个正确的命题,并证明这个命题.①AD=BC;②MN⊥BC;③AM=DM.查看答案和解析>>
科目:初中数学 来源: 题型:
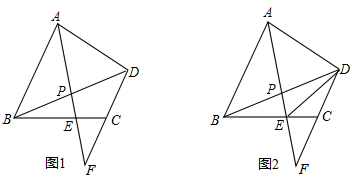
| AP | PE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com