
如图,四边形ABCD与四边形AEFG都是菱形,点C在AF上,点E,G分别在BC,CD上,若∠BAD=1350,∠EAG=750,则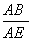 = .
= .

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
已知反比例函数y= (x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y=
(x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y= (x>0)的图象相交于点F(p,q).
(x>0)的图象相交于点F(p,q).
(1)当F点恰好为线段的中点时,求直线AF的解析式 (用含a的代数式表示);
(2)若直线AF分别与x轴、y轴交于点M、N,当q=-a2+5a时,令S=S△ANO+S△MFO(其中O是原点),求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
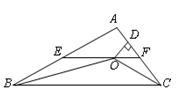
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:
①∠BOC=90º+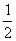 ∠A;
∠A;
②EF=BE+CF;
③设OD=m,AE+AF=n,则S△AEF=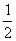 mn;
mn;
④EF是△ABC的中位线.
其中正确的结论是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com