
 如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB.
如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB.分析 (1)由同弧的圆周角相等即可得出∠ACE=∠DBE,结合∠AEC=∠DEB,即可证出△AEC∽△DEB;
(2)设⊙O的半径为r,则CE=2r-2,根据垂径定理以及三角形相似的性质即可得出关于r的一元一次方程,解方程即可得出r值,此题得解.
解答 (1)证明:∵∠AEC=∠DEB,∠ACE=∠DBE,
∴△AEC∽△DEB.
(2)解:设⊙O的半径为r,则CE=2r-2.
∵CD⊥AB,AB=8,
∴AE=BE=$\frac{1}{2}$AB=4.
∵△AEC∽△DEB,
∴$\frac{AE}{DE}=\frac{CE}{BE}$,即$\frac{4}{2}=\frac{2r-2}{4}$,
解得:r=5.
点评 本题考查了垂径定理以及相似三角形的判定与性质,根据相似三角形的性质找出方程是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
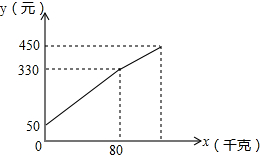 李大爷按每千克2.1元批发了一批蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降低出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
李大爷按每千克2.1元批发了一批蜜橘到镇上出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降低出售.售出蜜橘千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com