
如图1,在正方形ABCD中,AB=1,点E在AB延长线上,联结CE、DE,DE交边BC于点F,设BE ,CF
,CF .
.
图1
(1)求 关于
关于 的函数解析式,并写出
的函数解析式,并写出 的取值范围;
的取值范围;
(2)如图2,对角线AC、BD的交点记作O,直线OF交线段CE于点G,求证: ;
;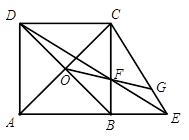
图2
(3)在(2)的条件下,当 时,求
时,求 的值.
的值.
(1)
 的取值范围是
的取值范围是
(2)略.
(3) ,
,
解析试题分析:(1)由正方形ABCD可得, ,则
,则  ,
,
即
(2)由(1)的结论得:
又

 ,即
,即 ,
,
根据正方形ABCD的性质得 ,∴△OCF∽△EAC
,∴△OCF∽△EAC
故 .
.
(3)在 △
△ 中,利用勾股定理得
中,利用勾股定理得
∵ ,
, 是公共角,
是公共角, , ∴根据相似三角形的性质三边对应成比例得
, ∴根据相似三角形的性质三边对应成比例得 ∴
∴
解得 ,
,
试题解析:(1)正方形ABCD中,DC∥AB,
∴ , 即
, 即 . (2分)
. (2分)
∴
 的取值范围是
的取值范围是 ; (2分)
; (2分)
(2)∵ ,
,
∴ (2分)
(2分)
又∵
∴△OCF∽△EAC (2分)
∴ (1分)
(1分)
(3)在 △
△ 中,
中, (1分)
(1分)
∵ ,
, 是公共角,
是公共角,
∴△OCG∽ △ECA (2分)
∴
∴ , 解得
, 解得 ,
, (2分)
(2分)
经检验 ,
, 都是满足方程的解
都是满足方程的解
答(略)
考点:1.相似三角形的判定。2.相似三角形的性质。


科目:初中数学 来源: 题型:解答题
(1)如图所示,如果你的位置在点A,你能看到后面那座高大的建筑物吗?为什么?
(2)如果两楼之间相距MN= m,两楼的高各为10m和30m,则当你至少与M楼相距多少m时,才能看到后面的N楼?
m,两楼的高各为10m和30m,则当你至少与M楼相距多少m时,才能看到后面的N楼?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)当点P在线段AB上时,求证:△APQ∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)当点P在线段AB上时,求证:△AQP∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图(1),∆ABC为等边三角形,AB=6,在直角三角板DEF中∠F=90°,∠FDE=60°,点D在边BC上运动,边DF始终经过点A,DE交AC于点G.
(1)求证:①∠BAD=∠CDG
②∆ABD∽∆DCG
(2)设BD=x,若CG= ,求x的值;
,求x的值;
(3)如图2,当D运动到BC中点时,点P为线段AD上一动点,连接CP,将线段CP绕着点C逆时针旋转60°得到CP' ,连接BP',DP',
①求∠CBP'的度数;②求DP'的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.
(1)求证:∠CBP=∠ABP;
(2)求证:AE=CP;
(3)当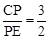 ,BP′=
,BP′= 时,求线段AB的长.
时,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
请在图中补全坐标系及缺失的部分,并在横线上写恰当的内容。图中各点坐标如下:A(1,0),B(6,0),C(1,3),D(6,2)。线段AB上有一点M,使△ACM∽△BDM,且相似比不等于1。求出点M的坐标并证明你的结论。
解:M( , )
证明:∵CA⊥AB,DB⊥AB,∴∠CAM=∠DBM= 度。
∵CA=AM=3,DB=BM=2,∴∠ACM=∠AMC( ),∠BDM=∠BMD(同理),
∴∠ACM= (180°- ) =45°。 ∠BDM=45°(同理)。
(180°- ) =45°。 ∠BDM=45°(同理)。
∴∠ACM=∠BDM。
在△ACM与△BDM中, ,
,
∴△ACM∽△BDM(如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com