
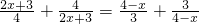 .
.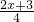 ,n=
,n= ,
, =n+
=n+ ,即(m-n)-(
,即(m-n)-( -
- )=0,
)=0,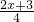 -
- =0,解得x=
=0,解得x= ,
,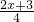 •
• -1=0,解得x1=0,x2=
-1=0,解得x1=0,x2= ,
, ,x3=
,x3= .
.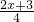 ,n=
,n= ,原方程化为m+
,原方程化为m+ =n+
=n+ ,即(m-n)-(
,即(m-n)-( -
- )=0,再通分,提公因式,得出两个方程,分别解每一个方程,结果要检验.
)=0,再通分,提公因式,得出两个方程,分别解每一个方程,结果要检验.

 备战中考寒假系列答案
备战中考寒假系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com