分析:①根据a
0=1(a≠0)以及负整数指数幂得到原式=-
÷
+1,再进行除法运算得原式=-1+1,然后进行实数的加法运算即可;
②根据积的乘方得到原式=(0.25×4)
2008=1
2008=1;
③先把单项式乘多项式得到原式=2x
2+6x-6x+3x
2,然后合并同类项即可;
④先根据平方差和完全平方公式展开得到原式=4x
2-y
2-(4x
2-4xy+y
2),然后去括号、合并同类项即可;
⑤先变形得到原式=[2x-(y-3z)][2x+(y-3z)],再根据平方差公式展开得到(2x)
2-(y-3z)
2=4x
2,然后再根据完全平方公式展开即可;
⑥根据平方差和完全平方公式展开得到原式=4(a
2+4a+4)-7(a
2-9)+3(a
2-2a+1),然后去括号、合并同类项即可.
解答:解:①原式=-
÷
+1=-1+1=0;
②原式=(0.25×4)
2008=1
2008=1;
③原式=2x
2+6x-6x+3x
2=5x
2;
④原式=4x
2-y
2-(4x
2-4xy+y
2)=4x
2-y
2-4x
2+4xy-y
2=4xy-2y
2;
⑤原式=[2x-(y-3z)][2x+(y-3z)]=(2x)
2-(y-3z)
2=4x
2-y
2+6yz-9z
2;
⑥原式=4(a
2+4a+4)-7(a
2-9)+3(a
2-2a+1)=4a
2+16a+64-7a
2+63+3a
2-6a+3=10a+130.
点评:本题考查了整式的混合运算:先根据乘法公式进行整式的乘除运算,然后去括号,合并同类项.也考查了a0=1(a≠0)以及负整数指数幂.



 名校课堂系列答案
名校课堂系列答案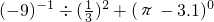 ;
;