
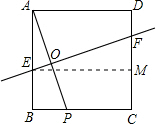
 解:过点E作EM⊥DC于M,
解:过点E作EM⊥DC于M,
|
| AB2+BP2 |


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省湖州市九年级中考一模调研测试数学试卷(解析版) 题型:解答题
如图①是矩形包书纸的示意图,虚线是折痕,四个角均为大小相同的正方形,正方形的边长为折叠进去的宽度.

(1)现有一本书长为25cm,宽为20cm,厚度是2cm,如果按照如图①的包书方式,并且折叠进去的宽度是3cm,则需要书包纸的长和宽分别为多少?(请直接写出答案).
(2)已知数学课本长为26 cm,宽为18.5cm,厚为1cm,小明用一张面积为1260cm2的矩形书包纸按如图①包好了这本书,求折进去的宽度.
(3)如图②,矩形ABCD是一张一个角(△AEF)被污损的书包纸,已知AB=30,BC=50,AE=12,AF=16,要使用没有污损的部分包一本长为19,宽为16,厚为6的字典,小红认为只要按如图②的剪裁方式剪出一张面积最大的矩形PGCH就能包好这本字典. 设PM=x,矩形PGCH的面积为y,当x取何值时y最大?并由此判断小红的想法是否可行.
查看答案和解析>>
科目:初中数学 来源:1989年第1届“五羊杯”初中数学竞赛初三试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com