
 已知直线y=-x+4与双曲线y=$\frac{k}{x}$(x>0)只有一个交点,将直线y=-x+4向上平移1个单位后与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,如图,则A点的坐标为( )
已知直线y=-x+4与双曲线y=$\frac{k}{x}$(x>0)只有一个交点,将直线y=-x+4向上平移1个单位后与双曲线y=$\frac{k}{x}$(x>0)相交于A,B两点,如图,则A点的坐标为( )| A. | (1,4) | B. | (1,5) | C. | (2,3) | D. | (2,4) |
分析 解方程$\frac{k}{x}$=-x+4,化为整式方程x2-4x+k=0,由于直线y=-x+4与双曲线y=$\frac{k}{x}$(x>0)只有一个交点,有△=0即可求出反比例函数解析式,求出直线y=-x+4向上平移1个单位后解析式,解两解析式联组立成的方程组即可求出A,B的坐标.
解答 解:解方程$\frac{k}{x}$=-x+4,
化为整式方程x2-4x+k=0,
∵直线y=-x+4与双曲线y=$\frac{k}{x}$(x>0)只有一个交点,
∴△=(-4)2-4k=0,
解得:k=4,
∴y=$\frac{4}{x}$,
直线y=-x+4向上平移1个单位后解析式为y=-x+5,
解方程组$\left\{\begin{array}{l}{y=\frac{4}{x}}\\{y=-x+5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=4}\\{{y}_{2}=1}\end{array}\right.$,
∴A(1,4),B(4,1),
故选A.
点评 本题主要考查了直线与双曲线的交点问题,直线的平移,了解直线与双曲线的只有一个交点,得到关于x的整式方程的判别式等于0求出k值是解题的关键.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:选择题
| 年利润(千万元) | 6 | 4 | 3 | 2 |
| 子公司个数 | 1 | 2 | 4 | 2 |
| A. | 4千万元,3千万元 | B. | 6千万元,4千万元 | C. | 6千万元,3千万元 | D. | 3千万元,3千万元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -a6•(-a)3=a8 | B. | (-3m-1)(3m-1)=-9m2+1 | ||
| C. | (x-2y)2=x2-4y2 | D. | [(-2x)2]3=-64x6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
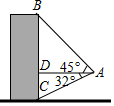 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的仰角为32°,已知该建筑物高BC为208米,求此时航拍无人机与该建筑物的水平距离AD(精确到0.1米)
如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的仰角为32°,已知该建筑物高BC为208米,求此时航拍无人机与该建筑物的水平距离AD(精确到0.1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com