Question

如图，AB∥CD，EF⊥AB于O ，∠2＝135°，求∠1的度数．

        

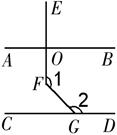
下面提供三个思路：

（1）过F作FH∥AB，

（2）延长EF交CD于I；

（3）延长GF交AB于K．

请你利用三个思路中的两个思路，求∠1的度数．

 

Answer 1

【答案】

135°

【解析】

试题分析：（2）先根据平行线的性质求得∠FIG的度数，由∠2的度数可得∠FGI的度数，再根据三角形的外角的性质即可求得结果；

（3）根据平行线的性质可得∠FKO的度数，再根据三角形的外角的性质即可求得结果.

（2）如图

∵AB∥CD，EF⊥AB

∴∠FIG＝90°

∵∠2＝135°

∴∠FGI＝45°

∴∠1=∠FIG+∠FGI＝135°；

∵AB∥CD，∠2＝135°

∴∠FKO＝180°-∠2＝45°

∵EF⊥AB

∴∠1=∠KOF+∠FKO＝135°.

考点：平行线的性质，

点评：辅助线问题是初中数学学习中的难点，能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力，因而这类问题在中考中比较常见，在各种题型中均有出现，一般难度较大，需多加关注.