
 如图,AB是半圆直径,半径OC⊥AB于点O,点D是弧BC的中点,连结CD、AD、OD,给出以下四个结论:
如图,AB是半圆直径,半径OC⊥AB于点O,点D是弧BC的中点,连结CD、AD、OD,给出以下四个结论:| A、①③ | B、②④ | C、①④ | D、①②③ |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| CD |
| OD |
| CE |
| CD |
| 1 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
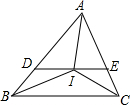 如图,△ABC中,IB,IC分别平分∠ABC,∠ACB,过I点作DE∥BC,分别交AB于D,交AC于E,给出下列结论:
如图,△ABC中,IB,IC分别平分∠ABC,∠ACB,过I点作DE∥BC,分别交AB于D,交AC于E,给出下列结论:| A、①②③ | B、②③④ |
| C、①③④ | D、①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
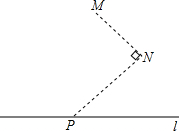 如图所示,在水渠l的同一侧有两个水池M与N,把水渠水先引到水池N,再由N引人水池M.连接MN,作∠MNP=90°,NP交l于点P,将水渠水由P放到N,再由N放到M,所行路径最短,对吗?如果不对,你是怎样设计的?写出你的设计方案.
如图所示,在水渠l的同一侧有两个水池M与N,把水渠水先引到水池N,再由N引人水池M.连接MN,作∠MNP=90°,NP交l于点P,将水渠水由P放到N,再由N放到M,所行路径最短,对吗?如果不对,你是怎样设计的?写出你的设计方案.查看答案和解析>>
科目:初中数学 来源: 题型:
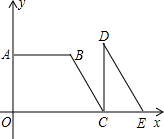 四边形OABC是直角梯形,△CDE是直角三角形,点A在y轴上,点C、E在x轴上,BC∥DE,抛物线y=-
四边形OABC是直角梯形,△CDE是直角三角形,点A在y轴上,点C、E在x轴上,BC∥DE,抛物线y=-| 2 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 12 |
| x |
| 4 |
| 3 |
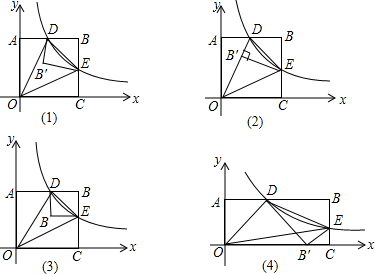
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com