
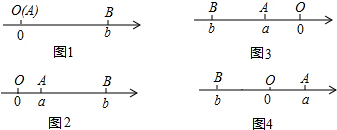
分析 ①根据数轴上两点间的距离=两个数之差的绝对值,算出即可;
②表示出AB的距离,根据绝对值等于2的数有2或-2两个,解答出即可;
③|x+1|+|x-3|的最小值,意思是x到-1的距离与到3的距离之和最小,那么x应在-1和2之间的线段上.
解答 解:①数轴上表示2和5的两点之间的距离是3,数轴上表示-2和-5的两点之间的距离是3,数轴上表示1和-3的两点之间的距离是4;
(2)数轴上表示x和-1的两点A和B之间的距离是|x+1|,如果|AB|=2,那么x为1或-3;
(3)当-1≤x≤2时,|x+1|+|x-2|的最小值是3.
故答案为:3;3;4;|x+1|;-3或1;-1≤x≤2.
点评 本题主要考查了数轴和绝对值,掌握数轴上两点间的距离=两个数之差的绝对值,绝对值是正数的数有2个


科目:初中数学 来源: 题型:选择题
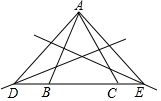 如图,在△ABC中,作为AB、AC的垂直平分线,分别交直线BC于点D、点E,连接AD、AE,已知∠DAE=82°,则∠BAC的度数为( )
如图,在△ABC中,作为AB、AC的垂直平分线,分别交直线BC于点D、点E,连接AD、AE,已知∠DAE=82°,则∠BAC的度数为( )| A. | 41° | B. | 49° | C. | 52° | D. | 54° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
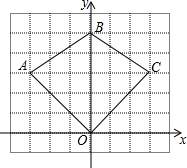 如图△COB是由△AOB经过某种变换后得到的图形,观察点A与点C的坐标之间的关系,解答下列问题:
如图△COB是由△AOB经过某种变换后得到的图形,观察点A与点C的坐标之间的关系,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com