
如图直线![]() 与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于D.
(1)当点M在AB上运动时,你认为四边形OCMD的周长是否发生变化?并说明理由;
(2)当点M运动到什么位置时,四边形OCMD的面积有最大值?最大值是多少?
(3)当四边形OCMD为正方形时,将四边形OCMD沿着x轴的正方向移动,设平移的距离为![]() ,正方形OCMD与△AOB重叠部分的面积为S.试求S与
,正方形OCMD与△AOB重叠部分的面积为S.试求S与![]() 的函数关系式并画出该函数的图象.
的函数关系式并画出该函数的图象.

解:(1)设点M的横坐标为x,则点M的纵坐标为-x+4(0<x<4,x>0,-x+4>0);
则:MC=-x+4=-x+4,MD=x=x;
∴C四边形OCMD=2(MC+MD)=2(-x+4+x)=8
∴当点M在AB上运动时,四边形OCMD的周长不发生变化,总是等于8;
(2)根据题意得:S四边形OCMD=MC?MD=(-x+4)? x=-x2+4x=-(x-2)2+4
∴四边形OCMD的面积是关于点M的横坐标x(0<x<4)的二次函数,并且当x=2,即当点M运动到线段AB的中点时,四边形OCMD的面积最大且最大面积为4;
(3)如图10(2),当![]() 时,
时,![]() ;
;
如图10(3),当![]() 时,
时,![]() ;
;
∴S与![]() 的函数的图象如下图所示:
的函数的图象如下图所示:

![]()
![]()


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
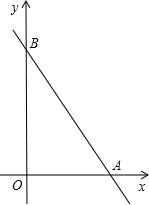 如图所示,直线AB与两坐标轴的交点坐标分别是A(6,0),B(0,8),O是坐标系原点.
如图所示,直线AB与两坐标轴的交点坐标分别是A(6,0),B(0,8),O是坐标系原点.查看答案和解析>>
科目:初中数学 来源: 题型:
(本小题满分14分)
如图所示,抛物线![]() 经过原点
经过原点![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,直线
,直线![]() 与两坐标轴分别交于
与两坐标轴分别交于![]() 、
、![]() 两点,与抛物线交于
两点,与抛物线交于![]() 、
、![]() 两点.
两点.

1.(1)求直线与抛物线的解析式;
2.(2)若抛物线在![]() 轴上方的部分有一动点
轴上方的部分有一动点![]() ,
,
求![]() 的面积最大值;
的面积最大值;
3.(3)若动点![]() 保持(2)中的运动路线,问是否存在点
保持(2)中的运动路线,问是否存在点
 ,使得
,使得![]() 的面积等于
的面积等于![]() 面积的
面积的![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;
的坐标;
若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
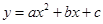 经过原点
经过原点 ,与
,与 轴交于另一点
轴交于另一点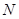 ,直线
,直线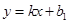 与两坐标轴分别交于
与两坐标轴分别交于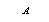 、
、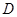 两点,与抛物线交于
两点,与抛物线交于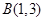 、
、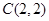 两点.
两点.
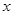 轴上方的部分有一动点
轴上方的部分有一动点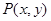 ,
,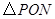 的面积最大值;
的面积最大值;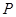 保持(2)中的运动路线,问是否存在点
保持(2)中的运动路线,问是否存在点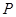 ,使得
,使得 的面积等于
的面积等于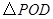 面积的
面积的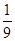 ?若存在,请求出点
?若存在,请求出点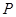 的坐标;
的坐标;查看答案和解析>>
科目:初中数学 来源:2012届广州市越秀区九年级第一学期期末调研测试数学卷 题型:解答题
(本小题满分14分)
如图所示,抛物线 经过原点
经过原点 ,与
,与 轴交于另一点
轴交于另一点 ,直线
,直线 与两坐标轴分别交于
与两坐标轴分别交于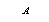 、
、 两点,与抛物线交于
两点,与抛物线交于 、
、 两点.
两点.
【小题1】(1)求直线与抛物线的解析式;
【小题2】(2)若抛物线在 轴上方的部分有一动点
轴上方的部分有一动点 ,
,
求 的面积最大值;
的面积最大值;
【小题3】(3)若动点 保持(2)中的运动路线,问是否存在点
保持(2)中的运动路线,问是否存在点 ,使得
,使得 的面积等于
的面积等于 面积的
面积的 ?若存在,请求出点
?若存在,请求出点 的坐标;
的坐标;
若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年广州市越秀区九年级第一学期期末调研测试数学卷 题型:解答题
(本小题满分14分)
如图所示,抛物线 经过原点
经过原点 ,与
,与 轴交于另一点
轴交于另一点 ,直线
,直线 与两坐标轴分别交于
与两坐标轴分别交于 、
、 两点,与抛物线交于
两点,与抛物线交于 、
、 两点.
两点.
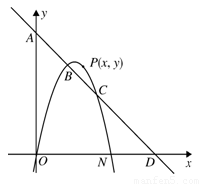
1.(1)求直线与抛物线的解析式;
2.(2)若抛物线在 轴上方的部分有一动点
轴上方的部分有一动点 ,
,
求 的面积最大值;
的面积最大值;
3.(3)若动点 保持(2)中的运动路线,问是否存在点
保持(2)中的运动路线,问是否存在点
 ,使得
,使得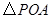 的面积等于
的面积等于 面积的
面积的 ?若存在,请求出点
?若存在,请求出点 的坐标;
的坐标;
若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com