Question

6．如图l，已知二次函数y=ax²-2ax+b的图象与x轴交于A，B两点，其中A（-1，0），且与直线l：y=$\sqrt{3}$x交于点C（4，m．）
（1）求二次函数的解析式；
（2）作CD⊥x轴于D，设点D关于直线l的对称点M，点M是否在（1）中的二次函数图象上，请说明理由；
（3）如图2，设CD的中点为点E，一条线段PQ沿直线l平移，且PQ=4，求QE+PD的最小值．

Answer 1

分析 （1）先求出点C的坐标，然后再用待定系数法就可解决问题；
（2）过点M作MH⊥x轴于H，连接OM，如图1，利用三角函数可得∠DOC=60°，然后根据对称性可得OM=OD=4，∠MOC=∠DOC=60°，则有∠MOH=60°，然后在Rt△HOM中运用三角函数可求出MH、OH，从而得到点M的坐标，然后把点M的坐标代入抛物线的解析式进行验证，即可解决问题；
（3）过点E作EF∥OC，交x轴于点F，连接PM，如图2，则有∠EFD=∠COD=60°，然后在Rt△EDF中运用三角函数可求出DF、EF，从而可证到四边形EFPQ是平行四边形，则有QE=PF．根据对称性可得PM=PD，则有QE+PD=PF+PM．根据两点之间线段最短可知：当M、P、F三点共线时，QE+PD=PF+PM最小，最小值为MF长，然后只需在Rt△MHF中运用勾股定理即可解决问题．

解答 解：（1）当x=4时，y=$\sqrt{3}$x=4$\sqrt{3}$，则点C（4，4$\sqrt{3}$）．
把点A（-1，0）、C（4，4$\sqrt{3}$）代入y=ax²-2ax+b，得
$\left\{\begin{array}{l}{a+2a+b=0}\\{16a-8a+b=4\sqrt{3}}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=\frac{4\sqrt{3}}{5}}\\{b=-\frac{12\sqrt{3}}{5}}\end{array}\right.$．
∴二次函数的解析式为y=$\frac{4\sqrt{3}}{5}$x²-$\frac{8\sqrt{3}}{5}$x-$\frac{12\sqrt{3}}{5}$；

（2）点M不在（1）中的二次函数图象上．
理由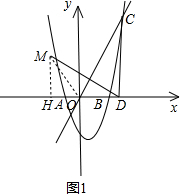：过点M作MH⊥x轴于H，连接OM，如图1，
在Rt△ODC中，tan∠DOC=$\frac{CD}{OD}$=$\frac{4\sqrt{3}}{4}$=$\sqrt{3}$，
∴∠DOC=60°，
∵点D与点M关于OC对称，
∴OM=OD=4，∠MOC=∠DOC=60°．
∴∠MOH=180°-60°-60°=60°．
在Rt△HOM中，MH=MO•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$，
OH=MO•cos60°=4×$\frac{1}{2}$=2，
∴点M的坐标为（-2，2$\sqrt{3}$）．
当x=-2时，y=$\frac{4\sqrt{3}}{5}$×（-2）²-$\frac{8\sqrt{3}}{5}$×（-2）-$\frac{12\sqrt{3}}{5}$=4$\sqrt{3}$≠2$\sqrt{3}$，
∴点M不在（1）中的二次函数图象上；

（3）过点E作EF∥OC，交x轴于点F，连接PM，如图2，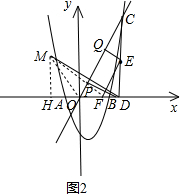
则有∠EFD=∠COD=60°．
∵E是CD的中点，
∴DE=$\frac{1}{2}$CD=2$\sqrt{3}$．
在Rt△EDF中，tan60°=$\frac{DE}{DF}$，sin60°=$\frac{ED}{EF}$，
∴$\sqrt{3}$=$\frac{2\sqrt{3}}{DF}$，$\frac{\sqrt{3}}{2}$=$\frac{2\sqrt{3}}{EF}$，
∴DF=2，EF=4，
∴PQ=EF，
∴四边形EFPQ是平行四边形，
∴QE=PF．
∵点D与点M关于OC对称，
∴PM=PD，
∴QE+PD=PF+PM．
根据两点之间线段最短可知：
当M、P、F三点共线时，QE+PD=PF+PM最小，最小值为MF长．
在Rt△MHF中，MF=$\sqrt{M{H}^{2}+H{F}^{2}}$=$\sqrt{（2\sqrt{3}）^{2}+（2+4-2）^{2}}$=2$\sqrt{7}$，
即QE+PD的最小值为2$\sqrt{7}$．

点评 本题主要考查了运用待定系数法求二次函数的解析式、抛物线上点的坐标特征、平行四边形的判定与性质、轴对称性、两点之间线段最短、勾股定理等知识，通过平移，将没有公共端点的线段和最短问题转化为有公共端点的线段和最短问题，是解决第（3）小题的关键．