解:(1)作CH⊥x轴,
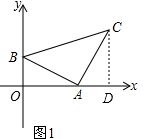
∴∠ADC=90°.
∴∠DAC+∠ACD=90°
∵∠BOA=90°,
∴∠ADC=∠BOA.
∵∠BAC=90°,
∴∠BAO+∠DAC=90°,
∴∠ACD=∠BAO.
在△CAD和ABO中
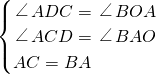
,
∴△CAD≌ABO(AAS),
∴AD=BO,CD=OA.
∵A(5,0)B(0,2),
∴OA=5,OB=2,
∴AD=2,CD=5,
∴OD=7.
∴C(7,5);
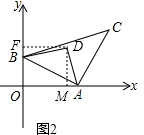
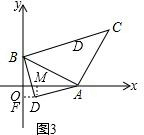
(2)如图2,当点D在第一象限∠BDA=90°,BD=DA时,作DF⊥y轴于F,DM⊥x轴于M,
∴∠DFB=∠DMO=∠DMA=90°.
∵∠AOF=90°,
∴四边形FOMD是矩形.
∴∠FDM=90°.
∵∠BDA=90°,
∴∠FDM=∠BDA,
∴∠FDM-∠BDM=∠BDA-∠BDM,
∴∠FDB=∠MDA.
在△BFD和△AMD中
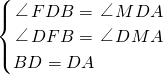
,
∴△BFD≌△AMD(AAS).
∴BF=MA,DF=DM.
∴四边形OMDF是正方形,
∴OF=DM.
∴2+BF=5-MA,
∴2+BF=5-BF,
∴BF=1.5,
∴OF=OM=3.5.
∴D(3.5,3.5);
如图2,当点D在第四象限∠BDA=90°,BD=DA时,作DF⊥y轴于F,DM⊥x轴于M,
∴∠DFB=∠DMO=∠DMA=90°.
∵∠AOF=90°,
∴四边形FOMD是矩形.
∴∠FDM=90°.
∵∠BDA=90°,
∴∠FDM=∠BDA,
∴∠FDM-∠BDM=∠BDA-∠BDM,
∴∠FDB=∠MDA.
在△BFD和△AMD中
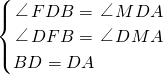
,
∴△BFD≌△AMD(AAS).
∴BF=MA,DF=DM.
∴四边形OMDF是正方形,
∴OF=OM.
∴2+OF=5-MO,
∴2+OF=5-OF,
∴OF=1.5,
∴OF=OM=1.5,
∴D(1.5,-1.5)
∴D(3.5,3.5)或D(1.5,-1.5);
故答案为:(3.5,3.5),(1.5,-1.5);
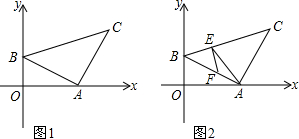
(3)作EM⊥AB,
∵FE⊥BC,
∴∠BEF=90°.
∵AB=AC,∠BAC=90°.
∴∠ABC=∠C=45°,
∴∠BFE=45°,
∴∠ABC=∠BFE,
∴BE=EF.
∵∠BEF=90,EM⊥AB,
∴BF=2EM.
∵∠AEC=75°,∠C=45°,
∴∠EAC=60°,
∴∠BAE=30°,
∴AE=2EM,
∴BF=AE.
分析:(1)作CH⊥x轴,由等腰直角三角形的性质就可以得出△CAD≌ABO,就有AD=BO,CD=OA,就可以求出OD而求出C的坐标;
(2)如图2,当点D在第一象限时,作DF⊥y轴于F,DM⊥x轴于M,证明△BFD≌△AMD就可以求出结论,如图3,当点D在第四象限时,作DF⊥y轴于F,DM⊥x轴于M,证明△BFD≌△AMD就可以求出结论.
(3)如图4,作EM⊥AB于M由等腰直角三角形的性质就可以得出BF=2EM,AE=2EM而得出结论.
点评:本题考查了坐标与图象的性质的运用,矩形的判定及性质的运用,正方形的判定及性质的运用,等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,解答时运用全等三角形的性质是关键.

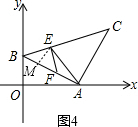
 已知:如图1:点A(5,0)B(0,2),AB=AC,∠BAC=90°.
已知:如图1:点A(5,0)B(0,2),AB=AC,∠BAC=90°.

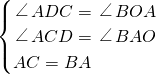 ,
, ,
,
 ,
,


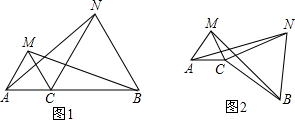 旋转成图2的情形,还有“AN=BM”的结论吗?如果有,请给予证明.
旋转成图2的情形,还有“AN=BM”的结论吗?如果有,请给予证明. 20、已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
20、已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.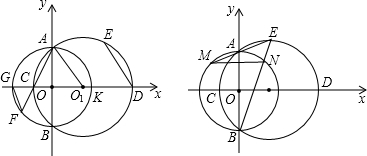 问:当点E在(不含端点A、B)上运动时,线段MN的长度是否会发生变化?试证明你的结论.
问:当点E在(不含端点A、B)上运动时,线段MN的长度是否会发生变化?试证明你的结论. 已知:如图,过点C(2,1)分别作x轴、y轴的平行线,交直线y=-x+4于B、A两点,若二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,且顶点在矩形ADBC内(包括三边上),则a的取值范围是
已知:如图,过点C(2,1)分别作x轴、y轴的平行线,交直线y=-x+4于B、A两点,若二次函数y=ax2+bx+c(a≠0)的图象经过坐标原点O,且顶点在矩形ADBC内(包括三边上),则a的取值范围是