
 已知:如图,在?ABCD中,E,F在AC上,且AE=CF,过E,F作EG∥HF,分别交CD,AB于G,H.求证:EF与GH互相平分.
已知:如图,在?ABCD中,E,F在AC上,且AE=CF,过E,F作EG∥HF,分别交CD,AB于G,H.求证:EF与GH互相平分. 分析 由四边形ABCD 是平行四边形,得到AB∥CD,根据平行线的性质得到∠1=∠2,因为HF∥EG,得到∠3=∠4,由AE=CF,得出AF=CE,通过△AHF≌△CGE,得到HF=EG,推出四边形EHFG是平行四边形,即可得出结论.
解答 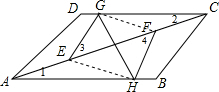 证明:∵四边形ABCD 是平行四边形,
证明:∵四边形ABCD 是平行四边形,
∴AB∥CD,
∴∠1=∠2,
∵HF∥EG,
∴∠3=∠4,
∵AE=CF,
∴AE+EF=CF+EF,
即:AF=CE,
在△AHF与△CGE中,
$\left\{\begin{array}{l}{∠1=∠2}\\{AF=CE}\\{∠4=∠3}\end{array}\right.$,
∴△AHF≌△CGE,
∴HF=EG,
∴四边形EHFG是平行四边形,
∴EF与GH互相平分.
点评 本题考查了平行四边形的判定和性质,全等三角形的判定与性质,熟记平行四边形的判定定理是解题的关键.


科目:初中数学 来源:2016-2017学年广西北海市七年级上学期期末教学质量检测数学试卷(解析版) 题型:填空题
为抄近路践踏草坪是一种不文明现象.请你用几何知识解释出现这一种现象的原因:____________________.
查看答案和解析>>
科目:初中数学 来源:2017届广东省佛山市顺德区九年级第一次模拟考试数学试卷(解析版) 题型:判断题
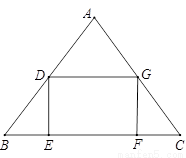
如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,S四边形DEFG=y.
(1)填空:自变量x的取值范围是___________;
(2)求出y与x的函数表达式;
(3)请描述y随x的变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一边上的中线 | B. | 一边上的高 | C. | 一角的平分线 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某村有一个四边形池塘,它的四个顶点A,B,C,D处均有一棵大树、村里准备开挖池塘建鱼塘.想使池塘的面积扩大一倍,又想保持大树在池塘边不动,并要求扩建后的池塘成平行四边形的形状,请问能否实现这一设想?若能,请你设计出所要求的平行四边形;若不能,请说明理由.
如图,某村有一个四边形池塘,它的四个顶点A,B,C,D处均有一棵大树、村里准备开挖池塘建鱼塘.想使池塘的面积扩大一倍,又想保持大树在池塘边不动,并要求扩建后的池塘成平行四边形的形状,请问能否实现这一设想?若能,请你设计出所要求的平行四边形;若不能,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-y={(\sqrt{-y})^2}(y<0)$ | B. | $-7={(\root{3}{-7})^3}$ | C. | $-7={(\sqrt{-7})^2}$ | D. | $-11=-\sqrt{(-11}{)^2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com