练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图中，AD⊥BC于D，AE是∠BAC的平分线，∠B=70°，∠C=34°，则∠DAE=________．

    答案：18°
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图甲，在△ABC中，AD⊥BC于D，AE平分∠BAC．
    （1）若∠B=30°，∠C=70°，则∠DAE=
     
    ；
    （2）若∠C-∠B=30°，则∠DAE=
     
    ；
    （3）若∠C-∠B=a（∠C＞∠B），求∠DAE的度数（用含a的代数式表示）；
    （4）如图乙，当∠C＜∠B时我们发现上述结论不成立，但为了使结论的统一与完美，我们不妨规定：角度也有正负，规定顺时针为正，逆时针为负．例如：∠DAE=-18°，则∠EAD=18°，作出上述规定后，上述结论还成立吗？
     
    ；若∠DAE=-7°，则∠B-∠C=
     
    °．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    24、如图：△ABC中，AD⊥BC于D，点E在AD上，△ADC和△BDE是等腰三角形，EC=5cm，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    15、已知，如图，锐角△ABC中，AD⊥BC于D，H为垂心（三角形三条高线的交点）；在AD上有一点P，且∠BPC为直角．
    求证：PD2=AD•HD

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

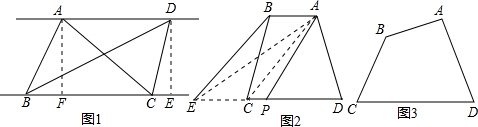
    （1）自主阅读：如图1，AD∥BC，连接AB、AC、BD、CD，则S△ABC=S△BCD．
    证明：分别过点A和D，作AF⊥BC，DE⊥BC
    由AD∥BC，可得AF=DE．
    又因为S△ABC=
    1
    2
    ×BC×AF，S△BCD=
    1
    2
    ×    BC×DE
    所以S△ABC=S△BCD
    由此我们可以得到以下的结论：像图1这样，
    同底等高的两三角形面积相等
    同底等高的两三角形面积相等
    ．
    （2）结论证明：如果一条直线（线段）把一个平面图形的面积分成相等的两部分，我们把这条直线（线段）称为这个平面图形的一条面积等分线（段），如，平行四变形的一条对角线就是平形四边形的一条面积等分线段．
    ①如图2，梯形ABCD中AB∥DC，连接AC，过点B作BE∥AC，交DC延长线于点E，连接点A和DE的中点P，则AP即为梯形ABCD的面积等分线段，请你写出这个结论成立的理由：
    ②如图3，四边形ABCD中，AB与CD不平行，S△ADC＞S△ABC，过点A能否做出四边形ABCD的面积等分线（段）？若能，请画出面积等分线（用钢笔或圆珠笔画图，不用写作法），不要证明

    查看答案和解析>>

    同步练习册答案