
 点C的横坐标为1,AC=3
点C的横坐标为1,AC=3| 10 |
8
| ||
| 5 |
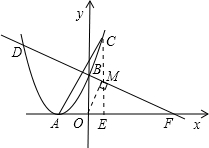 ∵抛物线上一点C的横坐标为1,
∵抛物线上一点C的横坐标为1,| 10 |
| 10 |
8
| ||
| 5 |
8
| ||
| 5 |
| OB2-OM2 |
4
| ||
| 5 |
| OM |
| BM |
| OF |
| BO |
| OF |
| 4 |
| ||||
|
|
|
| 1 |
| 2 |
|
|
|
| 9 |
| 2 |
| 25 |
| 4 |
| OB2+OF2 |
| 5 |
| OB2+OA2 |
| 5 |
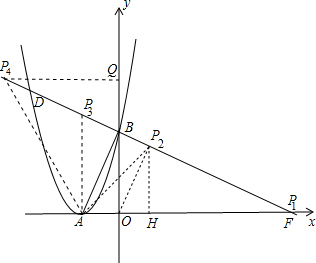
| 5 |
| 5 |
| 5 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
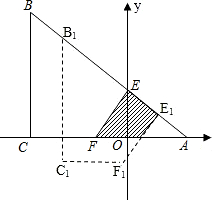 单位长度,平移中四边形BCFE与△AEF重叠的面积为S.
单位长度,平移中四边形BCFE与△AEF重叠的面积为S.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 4 |
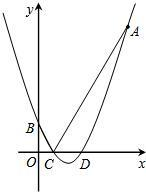
 ,与x轴相交于点F.
,与x轴相交于点F.| 4 |
| 5 |
| 5 |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 5 |
| 2 |
| 9 |
| 8 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 s向C点匀速移动,已知AC=4cm,BC=12cm,
s向C点匀速移动,已知AC=4cm,BC=12cm,查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
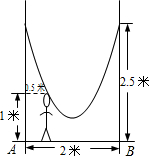 坐标系,根据题中提供的信息,求绳子所在抛物线的函数关系式;
坐标系,根据题中提供的信息,求绳子所在抛物线的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
| 1 |
| 2 |
| 1 |
| 2 |
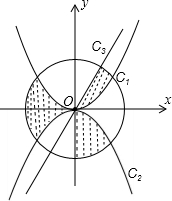
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com