
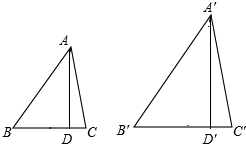
 如图所示,已知△ABC与△A′B′C′,AD⊥BC于D,A′D′⊥B′C′于D′,且$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠B=∠B′,试说明△ABC∽△A′B′C′.
如图所示,已知△ABC与△A′B′C′,AD⊥BC于D,A′D′⊥B′C′于D′,且$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,∠B=∠B′,试说明△ABC∽△A′B′C′. 分析 先证明△ABD∽△A′B′D′,得出∠BAD=∠B′A′D′,$\frac{AD}{A′D′}=\frac{AB}{A′B′}$,证出$\frac{AD}{A′D′}=\frac{AC}{A′C′}$,再证明Rt△ADC∽Rt△A′D′C′,得出对应角相等∠DAC=∠D′A′C′,得出∠BAC=∠B′A′C′,即可得出结论.
解答 证明:∵AD⊥BC于D,A′D′⊥B′C′于D′,
∴∠ADB=∠ADC=∠A′D′B′=∠A′D′C′=90°,
∵∠B=∠B′,
∴△ABD∽△A′B′D′,
∴∠BAD=∠B′A′D′,$\frac{AD}{A′D′}=\frac{AB}{A′B′}$,
∵$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,
∴$\frac{AD}{A′D′}=\frac{AC}{A′C′}$,
∴Rt△ADC∽Rt△A′D′C′,
∴∠DAC=∠D′A′C′,
∴∠BAC=∠B′A′C′,
又∵$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,
∴△ABC∽△A′B′C′.
点评 本题考查了相似三角形的判定与性质;熟练掌握相似三角形的判定与性质,并能进行推理论证是解决问题的关键.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分组 | 频数累计 | 频数 | 频率 |
| 0.55~1.05 | 正正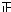 | 14 | 0.28 |
| 1.05~1.55 | 正正正 | 15 | 0.30 |
| 1.55~2.05 | 正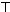 | 7 | 0.14 |
| 2.05~2.55 | 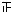 | 4 | 0.08 |
| 2.55~3.05 | 正 | 5 | 0.10 |
| 3.05~3.55 | 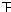 | 3 | 0.06 |
| 3.55~4.05 | 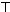 | 2 | 0.04 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com