
【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=1,ED=2. 
(1)求证:∠ABC=∠D;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
【答案】
(1)证明:∵AB=AC,
∴∠ABC=∠C,
∵∠C与∠D所对应的弧均为 ![]() ,
,
∴∠C=∠D,
∴∠ABC=∠D
(2)解:∵∠ABC=∠D,∠BAE=∠DAB,
∴△ABE∽△ADB,
∴ ![]() ,
,
即AB2=AE(AE+ED)=3,
解得:AB= ![]()
(3)答:直线FA与⊙O相切.理由如下:
连接OA,
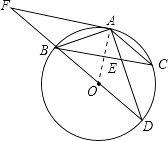
∵BD为⊙O的直径,
∴∠BAD=90°,
在Rt△ABD中,AB= ![]() ,AD=1+2=3,
,AD=1+2=3,
根据勾股定理得:BD=2 ![]() ,
,
∴OB=OA=AB= ![]() ,
,
∵BF=OB,
∴AB=FB=OB,即AB= ![]() OF,
OF,
∴∠OAF=90°,
则直线AF与⊙O相切.
【解析】(1)由AB=AC,利用等边对等角得到∠ABC=∠C,再由同弧所对的圆周角相等得到∠C=∠D,等量代换即可得证;(2)由(1)的结论与公共角相等,得到△ABE与△ADB相似,由相似得比例,即可求出AB的长;(3)直线FA与⊙O相切,理由为:连接OA,由BD为直径,得到∠BAD为直角,在Rt△ABD中,利用勾股定理求出BD的长,得到AB=OB=OA,根据BF=BO,得到AB等于FO的一半,确定出∠OAF为直角,即可得证.
【考点精析】本题主要考查了圆周角定理和切线的判定定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】2016年《政府工作报告》中提出了十大新词汇,为了解同学们对新词汇的关注度,某数学兴趣小组选取其中的A:“互联网+政务服务”,B:“工匠精神”,C:“光网城市”,D:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词.根据调查结果,该小组绘制了如下的两幅不完整的统计图. 
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名同学?
(2)条形统计图中,m= , n=;
(3)扇形统计图中,热词B所在扇形的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点D、E分别在△ABC的边AB、AC上,下列给出的条件中,不能判定DE∥BC的是( )
A.BD:AB=CE:AC
B.DE:BC=AB:AD
C.AB:AC=AD:AE
D.AD:DB=AE:EC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据 ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为 cm2 . (结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,M、N分别是边AB、AC的中点,在射线MN上取点D,使∠ADM=∠BAC,连接AD.
(1)如图1,当BC=3时,求DM的长.
(2)如图2,以AB为底边在AB的左侧作等腰△ABE,并且使顶角∠AEB=2∠BAC,连接EM.
①判断四边形AEMD的形状,并说明理由.
②设BC=x(x>0),四边形AEMD的面积为y,试用含x的式子表示y,并说明是否存在x的值,使得四边形AEMD的面积等于△ABC的面积?若存在,请求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
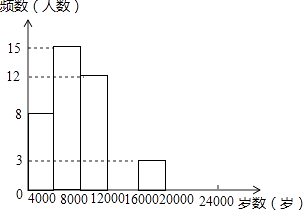
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的为( ) 
A.一定不是平行四边形
B.一定不是中心对称图形
C.可能是轴对称图形
D.当AC=BD时它是矩形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com