
【题目】如图,D、E、F、G四点在△ABC的三边上,其中DG与EF相交于点H.若 ∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=40°,则下列三角形相似的是( )
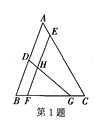
A.△BDG,△CEF B.△ABC,△CEF C.△ABC,△BDG D.△FGH,△ABC
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在真角坐标系中,矩形0ABC的顶点A,C在坐标轴上,点B(4,2);过点D(0,3)和E(6,0)的直线分别与AB、BC交于点M、N.
(1)求直线DE的函数表达式和点M,N的坐标;
(2)若函数y=![]() (k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(3)求△OMN的面积S;
(4)若函教y=![]() (k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.
(k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在3×3的正方形网格(每个小正方形的边长均为1)中有四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴(水平线为横轴),建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称.

(1)原点是 (填字母A,B,C,D );
(2)若点P在3×3的正方形网格内的坐标轴上,且与四个格点A,B,C,D,中的两点能构成面积为1的等腰直角三角形,则点P的坐标为 (写出可能的所有点P的坐标)
查看答案和解析>>
科目:初中数学 来源: 题型:
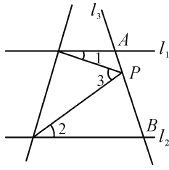
【题目】如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求:
(1)旋转中心;
(2)旋转角度数;
(3)图中经过旋转后能重合的三角形共有几对?若A、O、C三点不共线,结论还成立吗?为什么?
(4)求当△BOC为等腰直角三角形时的旋转角度;
(5)若∠A=15°,则求当A、C、B在同一条线上时的旋转角度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南充某制衣厂现有22名制作服装的工人,每天都制作某种品牌的衬衫和裤子,每人每天可制作这种衬衫3件或裤子5条。
(1)若该厂要求每天制作的衬衫和裤子配套,一件衬衫配两条裤子,则应各安排多少人分别制作衬衫和裤子?
(2)已知制作一件衬衫可获得利润30元,制作一条裤子可获得利润16元,在(1)的条件下,求该厂每天制作衬衫和裤子所获得的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
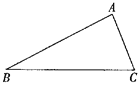
【题目】如图,在△ABC中,AB=4 cm,AC=2 cm.
(1)在AB上取一点D(D不与A、B重合),当AD=_________cm时,△ACD∽△ABC.
(2)在AC的延长线上取一点E,当CE=________cm时,△AEB∽△ABC.此时BE与DC有怎样的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:


如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级400名学生到郊外参加植树活动,已知用3辆小客车和1辆大客车每次可运送学生105人,用1辆小客车和2辆大客车每次可运送学生110人.
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若计划租小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满:
①请你设计出所有的租车方案;
②若小客车每辆租金150元,大客车每辆租金250元,请选出最省线的租车方案,并求出最少租金.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com