

���� ��1������λ��ͼ�ε����ʣ�����������PEFG��λ��������P'E'F'G'����ͼ1��ʾ��
��2����ͼ2����DEF������ڽ��������Σ���AD��ȡһ��M��ʹ��EM=MD���ɡ�DAE�ա�DCF���Ƴ���ADE=��CDF���ɡ�ADC=90�㣬�Ƴ���ADE=��CDF=15�㣬�Ƴ���MED=��MDE=15�㣬�Ƴ���AME=��MED+��MDE=30�㣬��AE=a����EM=DM=2a��AM=$\sqrt{3}$a���ɵ�$\sqrt{3}$a+2a=4���Ƴ�a=4��2-$\sqrt{3}$�����Ƴ�BE=BF=4��$\sqrt{3}$-1�����ɴ˼��ɽ�����⣮
��3���ܣ����ɣ���ͼ3�У������BEF��ֱ�������Σ�EF��BE��BF=3��4��5���ɡ�ABE�ס�DEF���ɵ�$\frac{DE}{AB}$=$\frac{DF}{AE}$=$\frac{EF}{BE}$=$\frac{3}{4}$��AB=4���Ƴ�DE=3��AE=1��DF=$\frac{3}{4}$���Ƴ�BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{17}$��EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=$\frac{3}{4}$$\sqrt{17}$��BF=$\sqrt{B{C}^{2}+C{F}^{2}}$=$\frac{5}{4}$$\sqrt{17}$���ɴ˼��ɽ�����⣮
��� �⣺��1����ͼ1��������P'E'F'G'��Ϊ����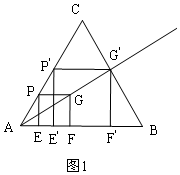
��2����ͼ2����DEF������ڽ��������Σ���AD��ȡһ��M��ʹ��EM=MD��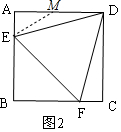
�ߡ�DEF�ǵȱ������Σ�
��DE=DF����EDF=60�㣬
��Rt��DAE��Rt��DCF��
$\left\{\begin{array}{l}{DE=DF}\\{DA=DC}\end{array}\right.$��
���DAE�ա�DCF��
���ADE=��CDF���ߡ�ADC=90�㣬
���ADE=��CDF=15�㣬
���MED=��MDE=15�㣬
���AME=��MED+��MDE=30�㣬
��AE=a����EM=DM=2a��AM=$\sqrt{3}$a��
��$\sqrt{3}$a+2a=4��
��a=4��2-$\sqrt{3}$����
��BE=BF=4��$\sqrt{3}$-1����
��S��DEF=16-2��$\frac{1}{2}$��4��4��2-$\sqrt{3}$��-$\frac{1}{2}$��4��$\sqrt{3}$-1����4��$\sqrt{3}$-1��=16��2$\sqrt{3}$-3����
��3���ܣ����ɣ���ͼ3�У������BEF��ֱ�������Σ�EF��BE��BF=3��4��5��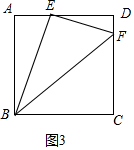
�ߡ�A=��D=��BEF=90�㣬
���AEB+��ABE=90�㣬��AEB+��DEF=90�㣬
���ABE=��DEF��
���ABE�ס�DEF��
��$\frac{DE}{AB}$=$\frac{DF}{AE}$=$\frac{EF}{BE}$=$\frac{3}{4}$����AB=4��
��DE=3��AE=1��DF=$\frac{3}{4}$��
��BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{17}$��EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=$\frac{3}{4}$$\sqrt{17}$��BF=$\sqrt{B{C}^{2}+C{F}^{2}}$=$\frac{5}{4}$$\sqrt{17}$��
���BEF����������
��S��DEF=$\frac{1}{2}$•BE•EF=$\frac{1}{2}$��$\sqrt{17}$��$\frac{3}{4}$$\sqrt{17}$=$\frac{51}{8}$��
���� ���⿼���ı����ۺ��⡢�ȱ������ε����ʡ������ε����ʡ�ֱ�������ε����ʡ����ɶ��������������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ӳ��ø����ߣ�ѧ�����ò����������̽�����⣬�����п�ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 36 | B�� | 6 | C�� | $\sqrt{6}$ | D�� | ��$\sqrt{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{10}$ | B�� | $\sqrt{12}$ | C�� | $\sqrt{14}$ | D�� | $\frac{\sqrt{17}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | -9 | D�� | 9 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com