
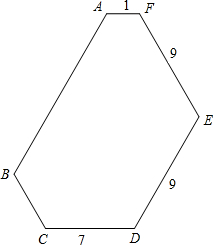
 如图,六边形ABCDEF的六个内角相等,若其连续四边长依次为1,9,9,7,(单位:),请你求出这个六边形的周长.
如图,六边形ABCDEF的六个内角相等,若其连续四边长依次为1,9,9,7,(单位:),请你求出这个六边形的周长.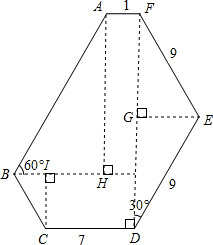 解:法一:如图,连接DF,则△DEF是等腰三角形,
解:法一:如图,连接DF,则△DEF是等腰三角形, (6-2)•180°=120°,
(6-2)•180°=120°, (180°-120°)=30°,
(180°-120°)=30°, =DF•
=DF• ,
, ,
, ×
× =18,
=18,


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见:
如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com