
若∠C= ,∠EAC+∠FBC=
,∠EAC+∠FBC=
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则 与
与 有何关系?并说明理由.
有何关系?并说明理由.
(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与 、
、 的关系是 .(用
的关系是 .(用 、
、 表示)
表示)
(3)如图③,若 ≥
≥ ,∠EAC与∠FBC的平分线相交于
,∠EAC与∠FBC的平分线相交于 ,
,  ;依此类推,则
;依此类推,则 = (用
= (用 、
、 表示)
表示)
(1) =
=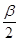 ;
;
(2)∠APB= ﹣
﹣
 ;
;
(3)∠A P5B= ﹣
﹣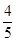
 .
.
解析试题分析:(1)过点C作CD∥AM,根据平行线相关定理即可; P
(2)利用三角形外角进行计算即可;
(3)类比(2)的做法进行计算.
试题解析:(1)过点C作CD∥AM,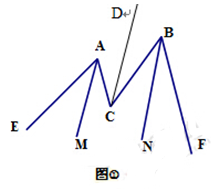
∵AM∥BN,
∴CD∥AM∥BN,
∴∠ACD=∠MAC,
∠BCD=∠CBN,
∴ =∠ACD+∠BCD =∠MAC +∠CBN=
=∠ACD+∠BCD =∠MAC +∠CBN= (∠EAC+∠FBC)=
(∠EAC+∠FBC)=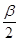 ,
,
∴ =
=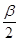 ;
;
(2)如图所示: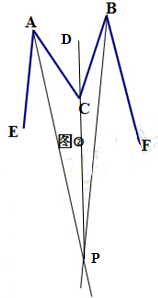
 (∠EAC+∠FBC)=
(∠EAC+∠FBC)= 



 ﹣
﹣
 ;
;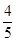 (∠EAC+∠FBC)=
(∠EAC+∠FBC)= 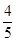

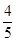

 ﹣
﹣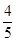
 .
.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
如图,EF//AD,∠1=∠2,∠BAC=80°.将求∠AGD的过程填写完整.
∵EF∥AD,
∴∠2= ( )
又∵∠1=∠2,
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=80°,
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知四边形ABCD,AD∥BC.点P在直线CD上运动(点P和点C,D不重合,点P,A,B不在同一条直线上),若记∠DAP,∠APB,∠PBC分别为 .
.
(1)当点P在线段CD上运动时,写出 之间的关系并说出理由;
之间的关系并说出理由;
(2)如果点P在线段CD(或DC)的延长线上运动,探究 之间的关系,并选择其中的一种情况说明理由.
之间的关系,并选择其中的一种情况说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com