
分析 多项式有公因式时,应先提取公因式,再对余下的多项式进行观察,若2项,考虑平方差公式,若3项,考虑完全平方公式和十字相乘法.
解答 解:(1)20a3-30a2=10a2(2a-3);
(2)16-(2a+3b)2
=42-(2a+3b)2
=(4+2a+3b)(4-2a-3b);
(3)-16x2y2+12xy3z=-4xy2(4x-3yz);
(4)5x2y-25x2y2+40x3y=5x2y(1-5y+8x);
(5)x2(a-b)2-y2(b-a)2
=x2(a-b)2-y2(a-b)2
=(a-b)2(x+y)(x-y);
(6)(a2+b2)2-4a2b2
=(a2+b2)2-(2ab)2
=(a2+b2+2ab)(a2+b2-2ab)
=(a+b)2(a-b)2;
(7)18b(a-b)2+12(b-a)3
=18b(b-a)2+12(b-a)3
=6(b-a)2(3b+2b-2a)
=6(b-a)2(5b-2a);
(8)x(x2+1)2-4x3
=x[(x2+1)2-(2x)2]
=x(x2+1+2x)(x2+1-2x)
=x(x+1)2(x-1)2;
(9)(x2-2x)2-3(x2-2x)
=(x2-2x)(x2-2x-3)
=(x2-2x)(x-3)(x+1);
(10)(2x-1)2-6(2x-1)+9
=(2x-1+3)2
=(2x+2)2
=4(x+1)2;
(11)16x4-72x2y2+81y4
=(4x2-9y2)2
=(2x+3y)2(2x-3y)2
(12)a5-a
=a(a4-1)
=a(a2+1)(a2-1)
=a(a2+1)(a+1)(a-1);
(13)25(x+y)2-9(x-y)2
=[5(x+y)+3(x-y)][5(x+y)-3(x-y)]
=(8x+2y)(2x+8y);
(14)m2-3m-28
=(m-7)(m+4);
(15)x2+x-20
=(x+5)(x-4).
点评 本题考查了因式分解的提公因式法、公式法及十字相乘法,需根据题目特点灵活选用各种方法对多项式进行因式分解.一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
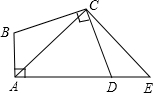 如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=CD,E是AD延长线上一点,若DE=AB=3cm,CE=4$\sqrt{2}$cm,连接AC,BD.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=CD,E是AD延长线上一点,若DE=AB=3cm,CE=4$\sqrt{2}$cm,连接AC,BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com