
| k |
| x |
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
| k |
| x |
| 10 |
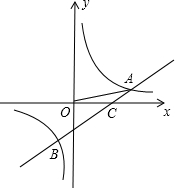 tan∠AOC=
tan∠AOC=| 1 |
| 3 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
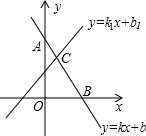 在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:
在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:| (1)一次函数的解析式就是一个二元一次方程; (2)点B的横坐标是方程①的解; (3)点C的坐标(x,y)中的x,y的值是方程组②的解.一次函数与不等式的关系;
|