练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．用配方法解一元二次方程x2+6x-3=0，原方程可变形为（　　）
    A．（x+3）2=3B．（x+3）2=6C．（x+3）2=12D．（x+3）2=9

    分析 移项后两边配上一次项系数一半的平方即可得．

    解答 解：∵x2+6x=3，
    ∴x2+6x+9=3+9，即（x+3）2=12，
    故选：C．

    点评 本题主要考查配方法解一元二次方程，熟练掌握配方法解一元二次方程的基本步骤是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    5．某种股票在7个月内销售增长率的变化情况如图所示，从图上看，下列结论不正确的是（　　）
    A．2～6月股票的销售量增长率逐渐变小
    B．7月份股票的销售量增长率开始回升
    C．这7个月中，每月的股票销量不断上涨
    D．这7个月中，股票销售量有上涨有下跌

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．如图所示，△AEB≌△DFC，AE⊥CB，DF⊥BC，∠C=28°，则∠A的度数为62°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．如果x1，x2是一元二次方程x2-6x-2=0的两个实数根，那么x1+x2-x1•x2的值是（　　）
    A．-8B．-4C．8D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．某班共有a名学生，其中男生人数占40%，那么女生人数为（　　）
    A．40%aB．（1-40%）aC．$\frac{a}{40%}$D．$\frac{a}{1-40%}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．问题情境：
    如图1，在菱形ABCD中，点E、F分别为AB，BC边上的点，连接AF，DE相交于点O，且∠AOE=∠ADC，试探究：AF与DE的数量关系．
    特例探究：
    如图2，当菱形ABCD是正方形时，AF与DE有怎样的数量关系呢？请你直接写出结论，不必证明；
    类比解答：
    类比特例探究的结论，猜想问题情境中AF与DE的数量关系，并说明理由；
    拓展延伸：
    将图1中的菱形ABCD改为?ABCD（如图3）其中AB=a，AD=b，点E、F、G、H分别为AB、BC、CD、DA边上的动点，连接EG、HF相交于点O，且∠HOE=∠ADC，试探究：EG与FH的数量关系，用含a、b的式子直接写出$\frac{EG}{FH}$的值，不必说明理由．

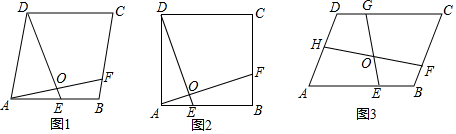
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．如图，以正方形ABCD的对角线AC为边作菱形AEFC，点E在边AB的延长线上，则∠FAE的度数等于（　　）
    A．15°B．22.5°C．30°D．37.5°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．已知抛物线y=x2-x-2与x轴的一个交点为（m，0），则代数式m2-m+2016的值为（　　）
    A．2017B．2018C．2019D．2020

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．我们知道：分式和分数有着很多的相似点，如类比分数的基本性质，我们得到了分式的基本性质：类比分数的运算法则，我们得到了分式的运算法则，等等．小学里，把分子比分母小的分数叫做真分数．类似地，我们把分子整式的次数小于分母整式的次数的分式称为真分式；反之，称为假分式，对于任何一个假分式都可以化成整式与真分式的和的形式．
    如：$\frac{x+1}{x-1}$=$\frac{x-1+2}{x-1}$=$\frac{x-1}{x-1}$+$\frac{2}{x-1}$=1+$\frac{2}{x-1}$；
    $\frac{2x-3}{x+1}$=$\frac{2x+2-5}{x+1}$=$\frac{2x+2}{x+1}$+$\frac{-5}{x+1}$=2+（-$\frac{5}{x+1}$）．
    （1）下列分式中：①$\frac{x-1}{x+1}$，②$\frac{{x}^{2}}{x-1}$，③$\frac{4y}{2{y}^{2}+1}$，④$\frac{{m}^{2}+3}{{m}^{2}-1}$，属于真分式的是③（填序号）；
    （2）将假分式$\frac{4a+5}{2a-1}$化成整式与真分式的和的形式为：
    $\frac{4a+5}{2a-1}$=2+$\frac{7}{2a-1}$，若假分式$\frac{4a+5}{2a-1}$的值为整数，则整数a的值为1或0或4或-3；
    （3）将假分式$\frac{{a}^{2}-3}{a+1}$化成整式与真分式的和的形式．

    查看答案和解析>>

    同步练习册答案