
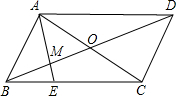
 如图?ABCD,O为对角线的交点,E为BC上一点,BE:EC=1:2,则BM:MO:OD=( )
如图?ABCD,O为对角线的交点,E为BC上一点,BE:EC=1:2,则BM:MO:OD=( )| A、2:2:3 | B、2:3:4 | C、1:1:2 | D、2:3:5 |
 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:阅读理解
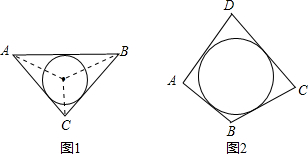 阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S△OAB+S△OBC+S△OCA
阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S△OAB+S△OBC+S△OCA| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2S |
| l |
查看答案和解析>>
科目:初中数学 来源: 题型:
 长度足够长),并利用已有总长为40米的铁围栏,设BC=x米,矩形车棚的面积为y平方米
长度足够长),并利用已有总长为40米的铁围栏,设BC=x米,矩形车棚的面积为y平方米查看答案和解析>>
科目:初中数学 来源: 题型:单选题
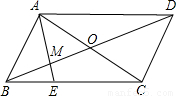
 如图?ABCD,O为对角线的交点,E为BC上一点,BE:EC=1:2,则BM:MO:OD=
如图?ABCD,O为对角线的交点,E为BC上一点,BE:EC=1:2,则BM:MO:OD=查看答案和解析>>
科目:初中数学 来源:2009-2010学年安徽省淮北市五校第二次联考九年级数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com