
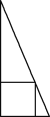
【题目】《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是________步.
【答案】![]()
【解析】
如图1,根据正方形的性质得:DE∥BC,则△ADE∽△ACB,列比例式可得结论;如图2,同理可得正方形的边长,比较可得最大值.
解:如图1,

∵四边形CDEF是正方形,
∴CD=ED,DE∥CF,
设ED=x,则CD=x,AD=12-x,
∵DE∥CF,
∴∠ADE=∠C,∠AED=∠B,
∴△ADE∽△ACB,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
x=![]() ,
,
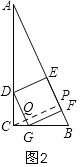
如图2,四边形DGFE是正方形,
过C作CP⊥AB于P,交DG于Q,
设ED=x,
S△ABC=![]() ACBC=
ACBC=![]() ABCP,
ABCP,
12×5=13CP,
CP=![]() ,
,
同理得:△CDG∽△CAB,
∴![]() =
=![]() ,
,
∴![]() =
=![]()
![]() ,
,
x=![]() <
<![]() ,
,
∴该直角三角形能容纳的正方形边长最大是![]() (步),
(步),
故答案为:![]() .
.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
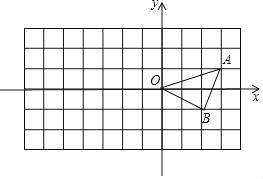
【题目】方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示.解答问题:
(1)请按要求对△ABO作如下变换:
①将△OAB向下平移2个单位,再向左平移3个单位得到△O1A1B1;
②以点O为位似中心,位似比为2:1,将△ABC在位似中心的异侧进行放大得到△OA2B2.
(2)写出点A1,A2的坐标: , ;
(3)△OA2B2的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四边形被一条对角线分割成两个三角形,如果被分割的两个三角形相似,我们把这条对角线称为该四边形的为相似对角线。
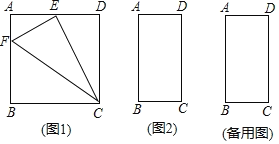
(1)如图1,正方形ABCD的边长为4,E为AD的中点,AF=1,连结CE,CF,求证:EF为四边形AECF的相似对角线。
(2)在四边形ABCD中,∠BAD=120°,AB=3,AC=![]() ,AC平分∠BAD,且AC是四边形ABCD的相似对角线,求BD的长。
,AC平分∠BAD,且AC是四边形ABCD的相似对角线,求BD的长。
(3)如图2,在矩形ABCD中,AB=6,BC=4,点E是线段AB(不取端点A,B)上的一个动点,点F是射线AD上的一个动点,若EF是四边形AECF的相似对角线,求BE的长.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连接AP并延长AP交CD于F点,连接CP并延长CP交AD于Q点.给出以下结论:①四边形AECF为平行四边形;②∠PBA=∠APQ;③△FPC为等腰三角形;④△APB≌△EPC;其中正确结论的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
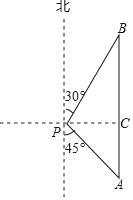
【题目】随着航母编队的成立,我国海军日益强大,2018年4月12日,中央军委在南海海域降重举行海上阅兵,在阅兵之前我军加强了海上巡逻,如图,我军巡逻舰在某海域航行到A处时,该舰在观测点P的南偏东45°的方向上,且与观测点P的距离PA为400海里;巡逻舰继续沿正北方向航行一段时间后,到达位于观测点P的北偏东30°方向上的B处,问此时巡逻舰与观测点P的距离PB为多少海里?(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,结果精确到1海里).
≈1.732,结果精确到1海里).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观测,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处,这样观测到的两个点A、B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、MN、M′N′均垂直于EF,MN=M′N′,露台的宽CD=GE.实际测得,GE=5米,EN=15.5米,NN′=6.2米.请根据以上信息,求出遮阳篷的宽AB是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和图形G,给出如下定义:在图形G上若存在两点M、N,使△PMN为正三角形,则称图形G为点P的T型线,点P为图形G的T型点,△PMN为图形G关于点P的T型三角形.若H(0,﹣2)是抛物线y=x2+n的T型点,则n的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
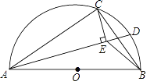
【题目】如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com