
【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
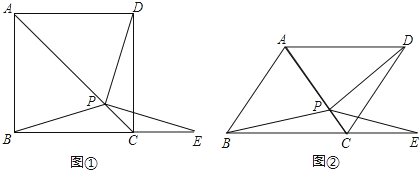
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
【答案】解:(1)证明:在正方形ABCD中,BC=DC,∠BCP=∠DCP=45°,
∵在△BCP和△DCP中,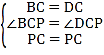 ,
,
∴△BCP≌△DCP(SAS)。
(2)证明:由(1)知,△BCP≌△DCP,
∴∠CBP=∠CDP。
∵PE=PB,∴∠CBP=∠E。∴∠DPE=∠DCE。
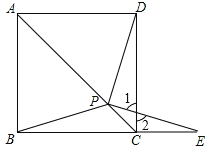
∵∠1=∠2(对顶角相等),
∴180°﹣∠1﹣∠CDP=180°﹣∠2﹣∠E,
即∠DPE=∠DCE。
∵AB∥CD,
∴∠DCE=∠ABC。
∴∠DPE=∠ABC。
(3)58
【解析】
试题分析:(1)根据正方形的四条边都相等可得BC=DC,对角线平分一组对角可得∠BCP=∠DCP,然后利用“边角边”证明即可。
(2)根据全等三角形对应角相等可得∠CBP=∠CDP,根据等边对等角可得∠CBP=∠E,然后求出∠DPE=∠DCE,再根据两直线平行,同位角相等可得∠DCE=∠ABC,从而得证。
(3)根据(2)的结论解答:
与(2)同理可得:∠DPE=∠ABC,
∵∠ABC=58°,∴∠DPE=58°。


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.在同一年出生的400人中至少有两人的生日相同
B.投掷一粒骰子,连投两次点数相同的概率与连投两次点数都为1的概率是相等的
C.从一副完整的扑克牌中随机抽取一张牌恰好是红桃K,这是必然事件
D.一个袋中装有3个红球,5个白球,任意摸出一个球是红球的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个同学周一到周五的体温测得的情况是36.2度,36.2度,36.5度,36.3度,36.4度,则这五个度数的众数和中位数分别是( )
A.36.3,36.2B.36.2,36.3C.36.2,36.4D.36.2,36.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接省运会在我市召开,市里组织了一个梯形鲜花队参加开幕式,要求共站60排,第一排40人,后面每一排都比前一排都多站一人,则每排人数y与该排排数x之间的函数关系式为____(x为1≤x≤60的整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用计算器计算数据13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A. 14.15 B. 14.16 C. 14.17 D. 14.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE.

(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:13=12 , 13+23=32 , 13+23+33=62 , 13+23+33+43=102…
(1)请叙述等式左边各个幂的底数与右边幂的底数之间有什么关系?
(2)利用上述规律,计算:13+23+33+43+…+1003 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com