
分析 根据实数的运算法则,负指数的性质,特殊角是三角函数的值计算即可.
解答 解:(1)|$\sqrt{3}$-2|+20100-($\frac{1}{3}$)-1+3tan30°=2-$\sqrt{3}$+1-3+3×$\frac{\sqrt{3}}{3}$=0;
(2)2sin30°+4cos30°•tan60°-cos245°=2×$\frac{1}{2}$+4×$\frac{\sqrt{3}}{2}$×$\sqrt{3}$-($\frac{\sqrt{2}}{2}$)2=$\frac{13}{2}$;
(3)$2sin45°+2cos60°-\sqrt{3}tan60°+\sqrt{18}$=2×$\frac{\sqrt{2}}{2}$+2×$\frac{1}{2}$-$\sqrt{3}•\sqrt{3}$+3$\sqrt{2}$=4$\sqrt{2}$-2;
(4)$\frac{{sin{{60}°}+3tan{{30}°}•cos{{60}°}}}{{({1-2tan{{45}°}})•tan{{60}°}}}$=$\frac{\frac{\sqrt{3}}{2}+3×\frac{\sqrt{3}}{3}×\frac{1}{2}}{(1-2×1)•\sqrt{3}}$=-1.
点评 本题考查了实数的运算法则,负指数的性质,特殊角是三角函数,熟练特殊角是三角函数是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
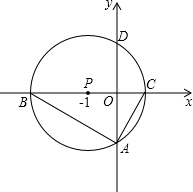 如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2,将△ABC绕点P旋转180°,得到△MCB.
如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2,将△ABC绕点P旋转180°,得到△MCB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com