
| |||||||||||
(1) |
测量步骤 ①在A楼的第二层选择测点C安置测倾器 ②设测倾器的度盘的圆心为E,在E点测得B楼的底部D的俯角为∠GED=α,测得B楼的顶部B的仰角∠GEB=β ③量出测倾器的高度CE=a m,量出测点C到地面的距离CF=b m 测量示意图如图所示
|
(2) |
解:因为EG∥FD,所以∠EDF=α,在Rt△EDF中, 解题指导:由于B的底部不能到达,所以A,B之间的水平距离不能测出,因此可选择A的任一层(第二层及以上)的某个合适的点为测点(注意:测点的选择要注意安全性).量出测点到地面的距离作为解直角三角形必备的边的条件,同时测出B楼的顶部的仰角和B楼的底部俯角,可求出B楼高. |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 学校C和D的距离相等(C、D所在位置如图所示),CA⊥AB于A,DB⊥AB于B,已知AB=10km,CA=8km,DB=6km.
学校C和D的距离相等(C、D所在位置如图所示),CA⊥AB于A,DB⊥AB于B,已知AB=10km,CA=8km,DB=6km.查看答案和解析>>
科目:初中数学 来源: 题型:
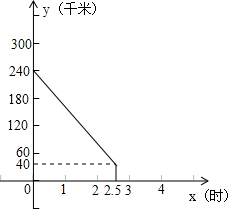 x(时)之间的函数图象.
x(时)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:
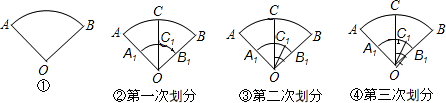
| 划分次数 | 扇形总数 |
| 1 | 6 |
| 2 | 11 |
| 3 | |
| 5 | |
| ????? | ??? |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 1 |
| a |
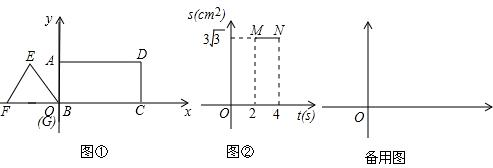
查看答案和解析>>
科目:初中数学 来源: 题型:
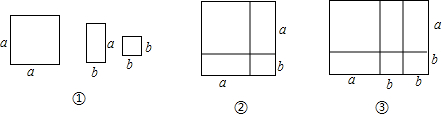
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com