Question

（1）请你在图1中画出正比例函数y=-2x的图象关于x轴对称的图象，并写出此图象的函数关系式为______；
（2）请你探究一次函数y=kx+b（k、b为常数，k≠0）的图象关于x轴对称的图象的函数关系式为______．（图2供探究用）

Answer 1

解：（1）设所求函数解析式为y=kx．
y=-2x经过点（1，-2），该点关于x轴的对称点为（1，2），
将（1，2）代入y=kx，得k=2．
所以直线y=-2x关于x轴对称的直线为y=2x，其图象如下：


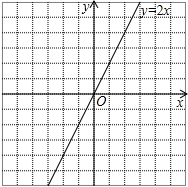
（2）设所求函数解析式为y=mx+n，
直线y=kx+b经过点（0，b），（1，k+b），
它们关于x轴对称的点分别为（0，-b），（1，-k-b），
将（0，-b），（1，-k-b）代入y=mx+n，
得-b=n，-k-b=m+n，
解得m=-k，n=-b，
所以一次函数y=kx+b（k、b为常数，k≠0）的图象关于x轴对称的图象的函数关系式为y=-kx-b．
故答案为y=2x；y=-kx-b．
分析：（1）设所求函数解析式为y=kx，先在直线y=-2x上任意取一点（1，-2），然后根据关于x轴对称的点，横坐标相同，纵坐标互为相反数求出这点的对应点的坐标，然后代入正比例函数解析式计算即可求出k值；
（2）设所求函数解析式为y=mx+n，先在直线y=kx+b上任意取两点（0，b），（1，k+b），然后根据关于x轴对称的点，横坐标相同，纵坐标互为相反数求出这两点的对应点的坐标，然后代入y=mx+n计算即可求出m、n的值．
点评：本题考查了一次函数图象与几何变换，根据点的对称规律求解直线的变化是此类题目常用的方法，熟记变化规律求解也可．