
| 2 |
| 3 |

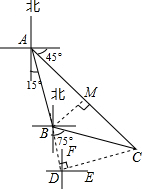 解:(1)过点B作BM⊥AC于点M,
解:(1)过点B作BM⊥AC于点M,| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 12 |
| 48 |


科目:初中数学 来源: 题型:
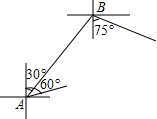 如图,在一次海上联合作战演习中,红方一艘侦察艇在A处发现在其北偏东30°方向,相距12海里的B处水面上,有蓝方一艘小艇正以每小时8海里的速度沿南偏东75°方向前进.若侦察艇以每小时16海里的速度,沿北偏东60°方向拦截蓝方的小艇.试问能否成功拦截?(
如图,在一次海上联合作战演习中,红方一艘侦察艇在A处发现在其北偏东30°方向,相距12海里的B处水面上,有蓝方一艘小艇正以每小时8海里的速度沿南偏东75°方向前进.若侦察艇以每小时16海里的速度,沿北偏东60°方向拦截蓝方的小艇.试问能否成功拦截?(| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ≈1.41
≈1.41 ≈1.73)
≈1.73)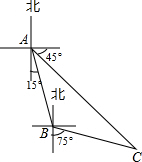
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com