|
|
|
解二元一次方程组的数学思想是什么？你是怎么理解的？
|
|
|
答案：
解析：
|
解二元一次方程组的数学思想是：消元思想．二元一次方程组中有两个未知数，如果消去其中一个未知数，那么就把二元一次方程组转化为我们熟悉的一元一次方程．我们可以先求出一个未知数，然后再求另一个未知数．这种将未知数的个数由多化少、逐一解决的思想，叫做消元思想．
|
练习册系列答案
相关习题
科目：初中数学
来源：青岛版(2014) 七年级下
题型：
|
|
|
如下图所示，如果b∥a，c∥a，那么b∥c吗？由此，可得平行线的判定方法：________．
|
|
|
查看答案和解析>>
科目：初中数学
来源：青岛版(2014) 七年级下
题型：
|
|
|
同一平面内已知直线AB和直线外一点P，过点P有________条直线与AB平行．
|
|
|
查看答案和解析>>
科目：初中数学
来源：青岛版(2014) 七年级下
题型：
|
|
|
已知 是方程组 的解，则3(b－a)－b2＝________．
|
|
|
查看答案和解析>>
科目：初中数学
来源：青岛版(2014) 七年级下
题型：
|
|
|
把方程7x－3y＝11写成用含x的代数式表示y的形式，结果是
|
| [ ] |
A． |
|
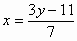
B． |
|
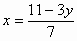
C． |
|
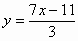
D． |
|
|
|
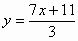
查看答案和解析>>
科目：初中数学
来源：青岛版(2014) 七年级下
题型：
|
|
|
用代入法解下列方程组：
(1)
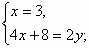
(2)
|
|
|
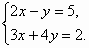
查看答案和解析>>
科目：初中数学
来源：青岛版(2014) 七年级下
题型：
|
|
|
已知4x－3y－6z＝0①，x＋2y－7z＝0②，且x，y，z均不为零，求 的值．
|
|
|
查看答案和解析>>
科目：初中数学
来源：青岛版(2014) 七年级下
题型：
|
|
|
某单位组织34人分别到井冈山和瑞金进行革命传统教育，到井冈山的人数是到瑞金的人数的2倍多1，求到两地的人数各是多少？
设到井冈山的人数为x，到瑞金的人数为y，请列出满足题意的方程组________．
|
|
|
查看答案和解析>>
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
