(1)证明:如图1,∵在△ABC中,∠ACB=90°,∠BAC=30°,
∴∠CBA=60°(直角三角形的两个锐角互余).
∵A′B′∥AC,
∴∠ACA′=∠CA′B′,
又由旋转的性质知,∠CA′B′=∠CAB=30°,
∴∠ACA′=∠CAB=30°,即θ=30°,
∴∠A′CB=∠ACB-θ=90°-30°=60°,
∴∠CDB=60°,
∴在△CDB中,∠DCB=∠CBD=∠BDC=60°,
∴△BCD是等边三角形;

(2)证明:如图2,由旋转的性质可知AC=CA
1,BC=CB
1,
∴

=

,
又由旋转的性质知,∠ACA
1=∠BCB
1∴△ACA
1∽△BCB
1,
∴S
△ACA′:S
△BCB′=AC
2:BC
2=
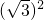
:1=3:1;
(3)解:如图,连接CP,当△ABC旋转到△A′B′C的位置时,
此时θ=∠ACA′=150°,EP=EC+CP=

AC+

A′B′=

×

a+

×2a=
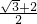
a.
即角θ150°时,EP长度最大,其最大值是
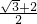
a.
分析:(1)由∠ACB=90°,∠BAC=30°得∠CBA=90°-30°=60°,根据旋转的性质可得∠CA′B′=∠CAB=30°,而A′B′∥AC,所以∠ACA′=∠CA′B′=30°,即θ=30°;
(2)由旋转的性质可证△ACA
1∽△BCB
1,利用相似三角形的面积比等于相似比的平方求解;
(3)连接CP,当E、C、P三点共线时,EP最长,根据图形求出此时的旋转角及EP的长.
点评:本题考查了旋转的性质,特殊三角形的判定与性质,相似三角形的判断与性质.关键是根据旋转及特殊三角形的性质证明问题.



 =
= ,
,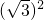 :1=3:1;
:1=3:1; AC+
AC+ A′B′=
A′B′= ×
× a+
a+ ×2a=
×2a=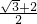 a.
a.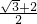 a.
a.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=