
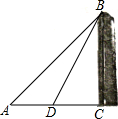
 津塔在天津大沽桥旁,是一座位于海河河畔的摩天大楼,某校数学兴趣小组要测量津塔的高度.如图,他们在点A处测得津塔的最高点B的仰角为45°,再往津塔方向前进至点D处测得津塔的高点B的仰角为60°,AD=142.6m.根据这个兴趣小组测得的数据,计算津塔的高度CB(
津塔在天津大沽桥旁,是一座位于海河河畔的摩天大楼,某校数学兴趣小组要测量津塔的高度.如图,他们在点A处测得津塔的最高点B的仰角为45°,再往津塔方向前进至点D处测得津塔的高点B的仰角为60°,AD=142.6m.根据这个兴趣小组测得的数据,计算津塔的高度CB(| 3 |
| BC |
| DC |
| 3 |
| x |
| x-142.6 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
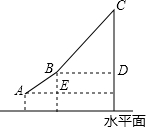 如图A、B、C表示建筑在一座比较险峻的景点上的三个缆车站的位置,已知A、B、C所处位置的海波高度分别是:130m,400m,1000m.钢缆AB与水平线AE的夹角为30°,钢缆BC与水平线BD的夹角为45°,求钢缆AB和BC的总长度.(精确到1m)
如图A、B、C表示建筑在一座比较险峻的景点上的三个缆车站的位置,已知A、B、C所处位置的海波高度分别是:130m,400m,1000m.钢缆AB与水平线AE的夹角为30°,钢缆BC与水平线BD的夹角为45°,求钢缆AB和BC的总长度.(精确到1m)查看答案和解析>>
科目:初中数学 来源: 题型:
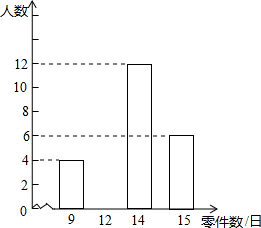 某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人进行调查.整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题:
某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人进行调查.整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
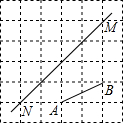 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com