Question

在半径为4的⊙O中，点C是以AB为直径的半圆的中点，OD⊥AC，垂足为D，点E是射线AB上的任意一点，DF//AB，DF与CE相交于点F，设E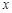F=，DF=．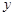

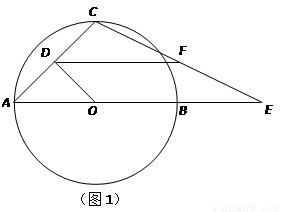
(1) 如图1，当点E在射线OB上时，求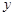关于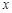的函数解析式，并写出自变量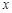的取值范围；

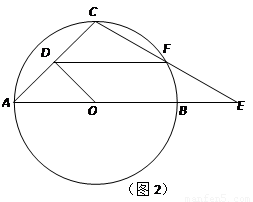
(2) 如图2，当点F在⊙O上时，求线段DF的长；

(3) 如果以点E为圆心、EF为半径的圆与⊙O相切，求线段DF的长．

 

Answer 1

【答案】

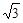(1) ，自变量x的取值范围为（2）2+2 （3）

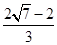
【解析】

试题分析：（1）联结OC，∵AC是⊙O的弦，OD⊥AC，∴OD=AD.

∵DF//AB，∴CF=EF，∴DF==．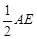

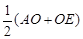∵点C是以AB为直径的半圆的中点，∴CO⊥AB．

∵EF=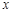，AO=CO=4,∴CE=2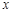,OE=.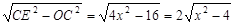

∴. 

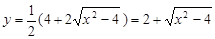自变量的取值范围为． 

（2）当点F在⊙O上时，联结OC、OF，EF=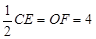，∴OC=OB=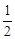AB=4．

∴DF=2+=2+2．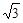 

（3）当⊙E与⊙O外切于点B时，BE=FE．∵，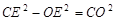

∴ ，

∴，）．

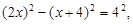
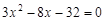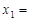
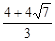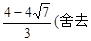∴DF=．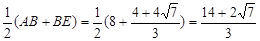 

当⊙E与⊙O内切于点B时，BE=FE．∵，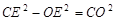

∴ ，

∴，）．

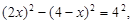
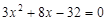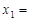
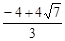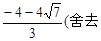∴DF=．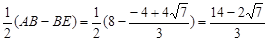 

当⊙E与⊙O内切于点A时，AE=FE．∵，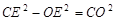

∴ ，

∴，）．

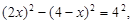
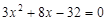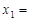
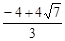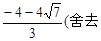∴DF=．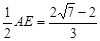 

考点：勾股定理，圆与圆外切，一元二次方程

点评：本题考查勾股定理，圆与圆外切，一元二次方程，解答本题需要掌握勾股定理的内容，熟悉圆与圆外切的概念和性质，掌握一元二次方程的解法