解:(1)由折叠的性质可得:∠EBD=∠DBC,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠EDB=∠DBC,
∴∠EBD=∠DBC,
∴EB=ED,
即△BED为等腰三角形;
(2)在△AEB与△FED中,
∵
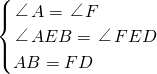
,
∴△AEB≌△FED(AAS),
∴AE=EF,
根据折叠可得:BF=BC=4,
设AE=x,
则EF=x,BE=BF-EF=4-x,
在Rt△AEB中,由勾股定理可得:AB
2+AE
2=EB
2,
代入得:3
2+x
2=(4-x)
2,
解得:x=

,
即AE=

.
分析:(1)根据折叠的性质可得∠EBD=∠DBC,然后根据平行线的性质得出∠EDB=∠DBC,继而可得∠EBD=∠DBC,证明EB=ED,即△BED为等腰三角形;
(2)根据折叠的性质易得△AEB≌△FED,设AE=x,得出BE=4-x,然后根据勾股定理,代入数据求解即可.
点评:此题主要考查了翻折变换的性质以及全等三角形的判定与性质和勾股定理等知识,利用已知设出AE的长,表示出BE的长是解题关键.

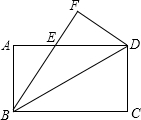
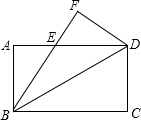 已知如图:长方形ABCD中,AB=3,BC=4,将△BCD沿BD翻折,点C落在点F处.
已知如图:长方形ABCD中,AB=3,BC=4,将△BCD沿BD翻折,点C落在点F处.
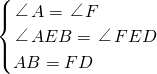 ,
, ,
, .
.
